Roberts Škapars. Pieprasījuma un piedāvājums elastības. Teorija. (e-grāmata)

Iepriekš tika noskaidrots, ka apskatāmās preces cena ir viens no svarīgākajiem piedāvājumu ietekmējošiem lielumiem, tādēļ ir svarīgi noteikt tās iedarbības pakāpi uz piedāvājumu. To nosaka ar piedāvājuma elastības palīdzību. Tā rāda, par cik procentiem mainās preces piedāvājums, ja piedāvātās preces cena mainās par vienu procentu. Piedāvājuma elastību aprēķina pēc šādas formulas:

(3.2.8)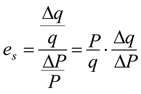

Tā kā piedāvājuma līknei normālas reakcijas gadījumā ir pozitīvs kāpums, tad tās elastība e_s ir pozitīva. Noteiksim piedāvājuma elastību grafiski. Pieņemam, ka ir dota piedāvājuma taisne S (3.2.6. attēls).

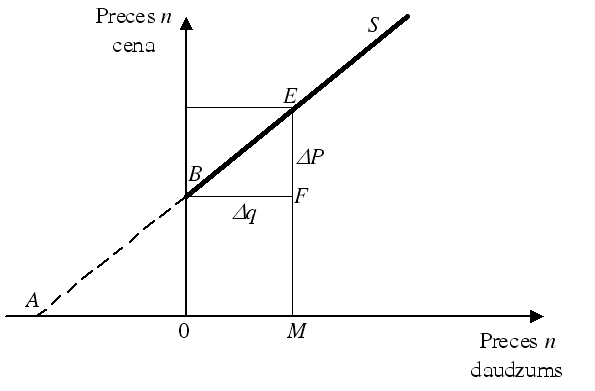
3.2.6. attēls. Piedāvājuma elastības grafiskā noteikšana

Uz tās kā sākuma pozīcija tiek skatīts punkts E. Ja cena pazeminās par Δc, tad piedāvājums samazinās par Δq.

Piedāvājuma elastība

(3.2.9)    ^.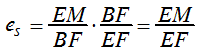

Izmantojam proporcionālo nogriežņu likumu un pārveidojam vienādojumu 3.4.2. Iegūstam šādu piedāvājuma elastības formulu:

(3.2.10)      .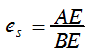

Piedāvājuma līknes dažādiem punktiem elastība ir atšķirīga, izņemot trīs gadījumus, kad tā ir konstanta visos piedāvājuma taisnes punktos (3.2.7. attēls).

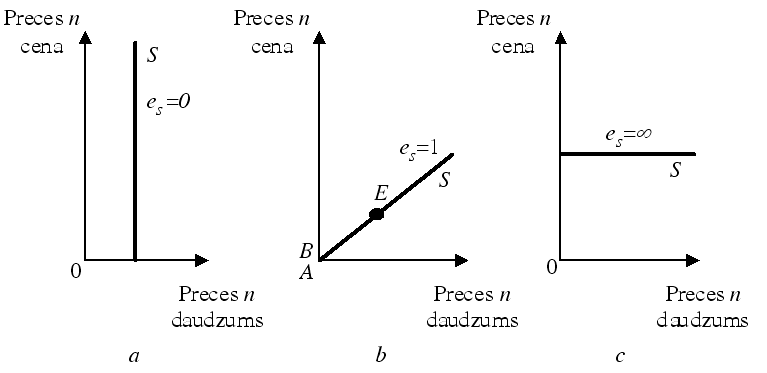
3.2.7. attēls. Piedāvājuma elastība visos taisnes punktos ir vienāda

1. Piedāvājuma taisne ir paralēla ordinātu asij, e_s=0 – pilnīgi neelastīgs piedāvājums (3.2.7. attēls a).

2. Piedāvājuma taisne iet caur koordinātu sistēmas sākumpunktu (3.2.7. attēls b), tad jebkurā taisnes punktā, neatkarīgi no tās stāvuma, saskaņā ar vienādojumu (3.2.10) elastība:

        

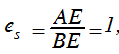
t.i., neitrāls piedāvājums (3.2.7. attēls b).

3. Piedāvājuma taisne ir paralēla abscisu asij, e_s= ∞ – pilnīgi elastīgs piedāvājums (3.2.7. attēls c).

Ja dota piedāvājuma taisne, tad elastība ir atšķirīga katrā taisnes punktā šādos gadījumos (3.2.8. attēls):

1. krusto ordinātu asi tās pozitīvajā zarā 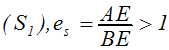 – elastīgs piedāvājums;

2. krusto ordinātu asi tās negatīvajā zarā 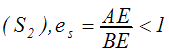 – neelastīgs piedāvājums.

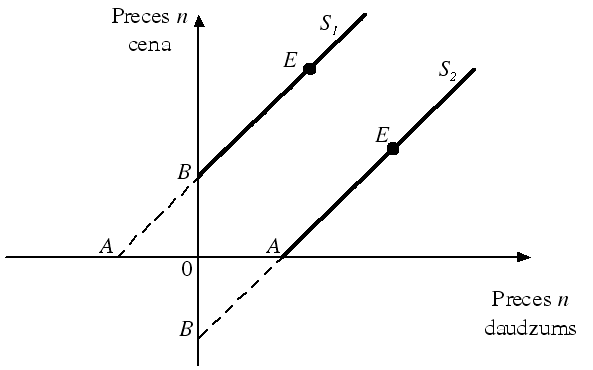
3.2.8. attēls. Piedāvājuma elastība dažādos taisnes punktos ir atšķirīga

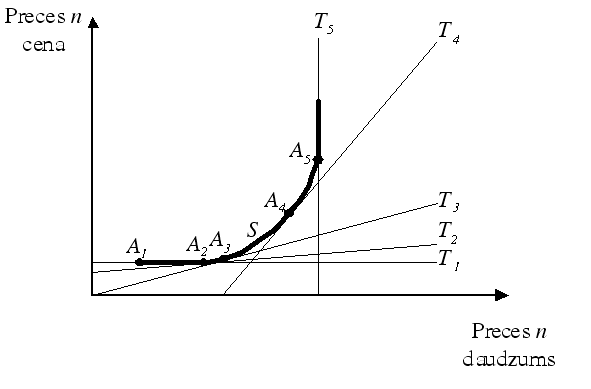
3.2.9. attēls. Piedāvājuma elastība

Iepriekš apskatītās likumsakarības elastības noteikšanā piedāvājuma taisnei der arī piedāvājuma līknei, jo caur katru tās punktu var novilkt pieskari, kura raksturo elastību šajā punktā. (3.2.9. attēls).

3.2.9. attēlā redzams, ka piedāvājuma līknes S dažādos punktos elastība ir atšķirīga:

• punktā A₁ tā ir vienlīdzīga ar bezgalību (e_s=∞);

• punktā A₂ tā ir lielāka par vienu (e_s>1);

• punktā A₃ tā ir vienlīdzīga ar vienu (e_s=1);

• punktā A₄ tā ir mazāka par vienu (e_s<1);

• punktā A₅ tā ir vienlīdzīga ar nulli (e_s=0).

Tātad, jo augstāka ir apskatāmās preces cena, jo zemāka ir piedāvājuma elastība.

Piedāvājuma elastību, ņemot vērā, ka tā nosaka apskatāmās preces cenas pārmaiņu ietekmi uz šīs preces piedāvājumu, tāpat kā pieprasījuma cenas elastību, sauc arī par tiešo elastību.

Piedāvājuma elastība, tāpat kā pieprasījuma elastība, ir atkarīga no laika perioda, kurā piedāvājums tiek skatīts. Piedāvājumu īsā laikā var raksturot divējādi. Pirmkārt, ja prece atrodas tirgus noliktavā, tad piedāvājums parasti paliek nemainīgs un nereaģē uz cenas pārmaiņām (pilnīgi neelastīgs piedāvājums). Tas ir sevišķi raksturīgs precēm, kuras ātri bojājas. Otrkārt, ja nav notikusi uzņēmuma paplašināšanās, preces ražošanu var palielināt tikai tad, ja uzņēmums nestrādā ar pilnu jaudu vai arī ir iespēja to ražot kādas citas preces vietā. Citādi ir ar preces ražošanas samazinājumu. Gandrīz vienmēr pastāv iespēja samazināt dotās preces ražošanu, slēdzot atsevišķas ražotnes un atlaižot strādniekus. Lielākas iespējas ir palielināt preces piedāvājumu, ja skatām to ilgā laika periodā, kad uzņēmums nepieciešamības gadījumā var uzsākt papildu ražotņu būvniecību un tādējādi lielos apjomos arī palielināt preces ražošanu. Šajā gadījumā piedāvājums reizēm var būt ļoti elastīgs.