15.nodaļa PUNKTVEIDA ĶERMEŅA SVĀRSTĪBU KUSTĪBA
( faktoloģija un cēlonība)
Līdztekus taisnlīnijas virzes kustībai x-ass pozitīvā vai negatīvā virzienā ļoti bieži novērojama arī taisnlīnijas svārstību kustība.
Par svārstībām sauc kustības, kas raksturojas ar laikā secīgiem un telpā ierobežotiem stāvokļiem.
Citiem vārdiem, svārstību kustībā ķermenis ieņem tikai noteiktus telpiskos stāvokļus un saka, ka kustība ir ierobežota telpā. Šīs ierobežotības dēļ tad arī novērojama ķermeņu ieņemto telpisko stāvokļu atkārtošanās laikā. Parasti svārstības aplūko kā kustību attiecībā pret t.s. līdzsvara stāvokli, kas ir savdabīgs kustības apraksta atskaites “ķermenis”.
Vienkārša svārstību kustība - harmoniskas svārstības
Īpašs gadījums ir harmoniskās svārstības, kuras matemātiski tiek aprakstītas ar sinusa funkciju un kā tādas ir svārstību kustības elementārsvārstības. Proti, no harmoniskajām svārstībām var sastādīt visas citas - kas jau ir atbilstoši sarežģītas svārstības.
x(t) = Xa sin [ 2p (t - to ) / T + jo(to) ] ,
kur T - svārstību periods, Xa - svārstību amplitūda, jo(to) - svārstību sākuma fāze
Taisnlīnijas harmonisko svārstību ļoti uzskatāms piemērs ir atsperei piekārta ķermeņa vertikālas svārstības, ja kāds ārējs ķermenis šīs svārstības ierosina un pēc tam arī uztur.
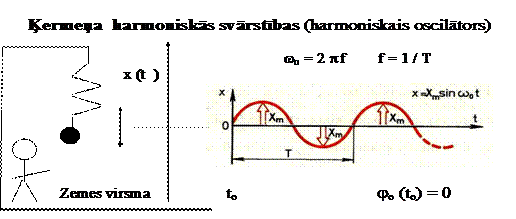
15.1.att.
Ja svārstības tiek tikai ierosinātas un tās turpmāk īstenojas no ārējiem ķermeņiem (iedarbībām) nosacīti neatkarīgi, tad runā par kustošā ķermeņa pašsvārstībām, kuras idealizētā gadījumā būtu nerimstošas, bet reāli vienmēr ir rimstošas svārstības (laika gaitā novērojam svārstību amplitūdas pakāpenisku samazināšanos). Nerimstošas svārstības īstenojas tad, ja ierosinātās svārstības atbilstoši uztur kāds ārējs ķermenis (uzspiestās svārstības).
Īpašs un praksē ļoti nozīmīgs gadījums ir tad, ja uz svārstošos ķermeni iedarbojas vēl kāds ķermenis un ierosina papildus svārstības ar citu, no sākotnējas pašsvārstību frekvences atšķirīgu frekvenci. Šai t.s. uzspiesto svārstību frekvencei mainoties, tiek novērota harmonisko svārstību rezonanses parādība.
Harmoniskās svārstības īstenojas kā periodiska divu ķermeņu savstarpējā attāluma mainība, kuras cēlonis ir noteiktas dotā ķermeņu pāra mijiedarbības īstenojums. Šīs mijiedarbības specifika raksturojas ar to, ka ķermeņiem atrodoties periodiski mainīgā attālumā vienam no otra, tie vienmēr savstarpēji pievelkas (tuvojas) un atgrūžas (attālinās) ar spēku, kas proporcionāls attālumam līdz ķermeņu līdzsvara stāvoklim, ap kuru notiek svārstības.

15.2.att.
15.1. Sarežģītas svārstību kustības
Līdzīgi kā virzes kustības gadījumā, arī svārstību kustībā esošs ķermenis var vienlaicīgi īstenot vairākas vienkāršas jeb elementāras, dažādu iedarbības avotu rosinātas harmoniskas svārstības. Kopumā ķermenis jau veic saliktu jeb sarežģītu svārstību kustību.
Ķermeņu sarežģītas svārstību kustības veidojas, ja tiek saskaitītas vienlaicīgi dažādos telpas virzienos īstenojošās dažādas harmoniskās svārstības (svārstības ar dažādām frkvencēm, amplitūdām un sākuma fāzēm).
Ir iespējamas ļoti daudzas dažādas konkrētas situācijas - atbilstoši ārkārtīgi liela svārstību kustību daudzveidīga.
Visas sarežģītās svārstības laika skatījumā var sagrupēt periodiskajās un neperiodiskajās svārstību kustībās.
Vienkārša periodiskā svērstību kustība ir harmoniskā svārstību kustība.
x (t) = Xa sin [ 2p (t - to ) / T + jo (to) ] ,
kur T - svārstību periods, Xa - svārstību amplitūda, jo (to) - svārstību sākuma fāze
Salīdzinoši vienkārša perodiska ķermeņa svārstību kustība ir tad, kad ķermenis vienlaicīgi veic harmoniskas svārstības divos dsavstarpēji perpendikulāros virzienos. Atkarībā no konkrētiem apstākļiem, kurus nosaka harmonisko svārstību frekvenču, amplitūdu un sākuma fāzu atšķirības, iegūstam raksturīgas ķermeņa periodiskas kustības telpā. Vienkāršākoajos gadījummos iegūst periodisku harmonisku taisnlīnijas svārstību kustību virzienā, kas atšķirīgs no atsevišķo divu svārstību virzieniem, citreiz - līklīnijas kustību plaknē pa eliptisku trjektoriju jeb ceļu. Īpašs gadījums ir periodiskas kustības pa riņķa līniju sintēze.
Sarežģīto kustību izpatnei vissvarīgākā ir sistēmiskās domāšanas pamatatziņa: veselais sastāv no kopsaistītām daļām.

