Mehānika profesionālajā izglītībā
| Vietne: | Profesionālajā izglītībā iesaistīto vispārizglītojošo mācību priekšmetu pedagogu kompetences paaugstināšana |
| Kurss: | FiziT009 : Vispārizglītojošā fizika profesionālajā izglītībā |
| Grāmata: | Mehānika profesionālajā izglītībā |
| Drukājis: | Vieslietotājs |
| Datums: | trešdiena, 2026. gada 11. marts, 01:58 |
Apraksts
Stundu sadalījums/plānojums - mehānika
Satura rādītājs
- 1. IEVADS
- 2. 1.nod. Mehānikas struktūra un saturs
- 3. 3.nod.Mehānikas struktūra makropasaulē_makets
- 4. 4.nod. Tematiskais stundu plānojums profesionālajā izglītībā 2 - mehānika
- 5. 5.nod. Pamatzināšanu saturs mehānikā
- 6. 6.nodaļa Cilvēks makropasaulē-ievads
- 7. 7.nodaļa Kermeņu kustību pamatveidi
- 8. 8.nod. Punktveida ķermeņu mehānika
- 9. 9.nod. Ķermeņu kustību daudzveidība
- 10. 10.nod. Kinētika
- 11. 11.nod. Ķermeņa virzes kustības dinamika
- 12. 12.nod. Ķermeņu impulss
- 13. 13.nod. Ķermeņu enerģija
- 14. 14.nod. Pāra ķermeņu dinamika
- 15. 15.nod.Ķermeņu svārstības
- 16. 16.nod. Stohastiskas svārstības
- 17. Nobeigums - karte

Mehānika profesionālajā izglītībā
A.Krons
Materiāls izstrādāts
ESF Darbības programmas 2007. - 2013.gadam
„Cilvēkresursi un nodarbinātība”
prioritātes 1.2. „Izglītība un prasmes”
pasākuma 1.2.1.„Profesionālās izglītības un vispārējo prasmju attīstība”
aktivitātes 1.2.1.2. „Vispārējo zināšanu un prasmju uzlabošana”
apakšaktivitātes 1.2.1.1.2. „Profesionālajā izglītībā iesaistīto pedagogu
kompetences paaugstināšana”
Latvijas Universitātes realizētā projekta
„Profesionālajā izglītībā iesaistīto vispārizglītojošo mācību priekšmetu pedagogu
kompetences paaugstināšana”
(Vienošanās Nr.2009/0274/1DP/1.2.1.1.2/09/IPIA/VIAA/003,
LU reģistrācijas Nr.ESS2009/88) īstenošanai
Ievads
Ap mums ir reālu daudzveidīgu fizikālu parādību pasaule, kuru veido mainīgu ķermeņu kopums. Visām fizikālām parādībām rast atbildes un skaidrojumus šodien nav iespējams. Tieši fizika, kā viena no dabaszinātņu nozarēm, var rast atbildes uz dažnedažādākajiem jautājumiem, kas nepieciešamas cilvēces turpmākai attīstībai un civilizācijas progresam.
Fizika – fundamentāla zinātniska TEORIJA par materiālās pasaules ķermeņu kustību telpā un laikā, kas atveidojas kā fizikālas parādības CILVĒKU APZIŅĀ.
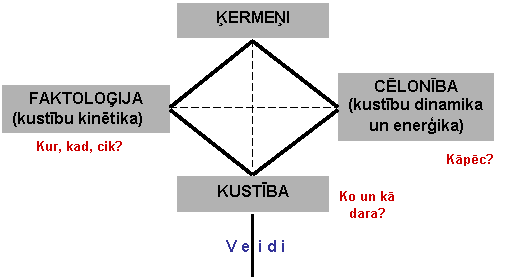
Cilvēks apzina apkārtējo pasauli, tajā notiekošās fizikālās parādības telpā un laikā. T E L P A - fizikālu ķermeņu savstarpējo novietojumu raksturojošo stāvokļu kopums. L A I K S - fizikālu ķermeņu mainību raksturojošo secīgo stāvokļu kopums. Cilvēks cenšas apzināt apkārtējo pasauli faktoloģiski (kas, kad, kur un kā notiek), noskaidro dabas parādību cēloņsakarības (kāpēc, kas tad, tur un tā notiek).
Viss pasaulē atrodas mainībā un kustībā. Katrs fizikāls ķermenis raksturojas ar savu iekšējo vidi, kas atrodas kopsaistībā (mijiedarbībā) caur savu robežvirsmu ar ārējo (apkārtējo) vidi. Tieši fizikālie jēdzieni s p ē k s un e n e r ģ i j a, kas radīti cilvēka apziņā, veiksmīgi kalpo visdažādāko pasaules fizikālo ķermeņu savstarpējo mijiedarbību aprakstam. Cēlonības problēmu risināšanas pamatā ir vispārīga atziņa, ka visa cēlonis ir visa kopsaistība.
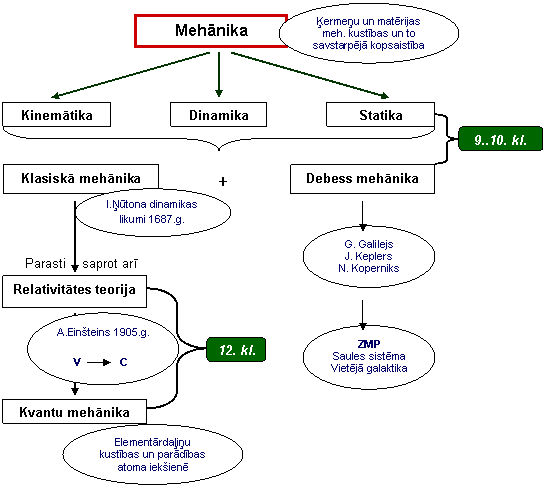
Dabaszinātņu, tehnikas un tehnoloģiju jomas ir plaši sazarotas. Arī fizikas nozare - mehānika - nav izņēmums. Mehānika ir fizikas centrālā un vispārīgā daļa - teorija par fizikālo ķermeņu savstarpējo novietojumu telpā un laikā, un šī novietojuma mainību jeb kustību. Mehānikā materiālās pasaules apzināšanai makro, mikro un mega līmeņos, lai skaidrotu fizikālas parādības, izman to fizikālus terminus: ķermeņi, kustība - stāvokļi, telpa, laiks un mijiedarbības, spēks, darbs, enerģija.
Materiālās pasaules apzināšanai makro, mikro un mega līmeņos cilvēki kā saprātīgas dom ājošas būtnes izmanto fizikas pamatjēdzienus (1.att.):
ājošas būtnes izmanto fizikas pamatjēdzienus (1.att.):
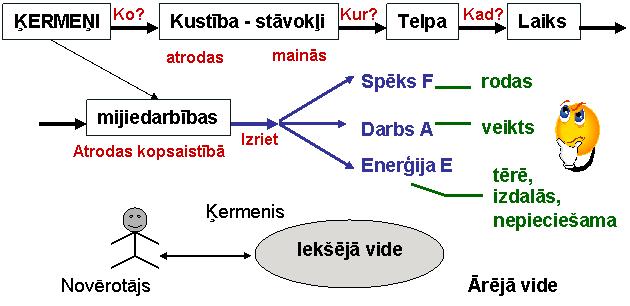
1.att. Ikviena vide ir noteiktu ķermeņu kopums
*
*
1.1.1. Punktveida ķermeņu mehānika ( noteiktas jeb determinētas un nenoteiktas jeb
2.1.1. Gāzveida un kondensētās vides – megapasaules, makropasaules
un mikropasaules ķermeņu veidotās vides. Vielas (gāzes,
šķidrumi, cietvielas) un starojumi.
2.1.2. Nepārtrauktas un diskrētas vides kustība ķermeņos (
2.1.3. Vielisko ķermeņu strukturālās pārvērtības, ķermeņu
fizikālās īpašības.
2.2. Vides pārneses mehānika:
iekšējās un ārējās vides kustība caur ķermeņa robežvirsmu - nepārtrauktas un diskrētas vides kustība (vielas pārnese caur gāzveida, šķidro un cieto ķermeņu robežvirsmām, vides pārneses procesi dabā un tehnikā, mikrodaļiņu emisija un absorbcija).
2.3.1. Ķermeņu iekšējās vides ārējās mehāniskās ierosas, to
raksturojums (harmoniskās svārstības kā vides
elementārierosa, impulsveida ierosas – kvazidaļiņas).
2.3.2. Vides ierosu izplate : kustības pārnese caur ķermeņu
robežvirsmām
(* Dr.fiz., asoc.prof. Andris Broks “Vispārizglītojošā Fizika – mehānika”
LU FMF Fizikas izglītības centrs 13.03.2011)
PASAULE ir mainīgu ķermeņu kopums


[LAIKS, mainība] [
(Mainību
Pārējās fizikas daļas ir saistītas ar dažādu ķermeņu dažādu kustību specifikas apzināšanu materiālās pasaules makro, mikro un mega līmeņos.
Saturs

Ieteicamās tēmas
Vektori
Vienm
Kust
Main
Pa
Pa
Vienm
Pa
(saist
Saist
Elast
Smaguma spēks -
Vispasaules gravitācijas spēks MZP
Keplera likumi
Sp
Elast
Reakt
Meh
Meh
Mehāniskās svārstības. Svārstību raksturlielumi.
Br
Rezonanse
Harmonisk
Ener
Meh
Vi
Garenvi
Ska
Doplera efekts
1.4. att. Mehānikas strukturālais sadalījums

Mācību priekšmeta mērķis un uzdevumi
1. Mācību priekšmeta mērķis ir pilnveidot izpratni par fizikālajām parādībām dabā un
tehnikā un attīstīt atbildīgu attieksmi pret cilvēka, sabiedrības un vides mijiedarbību.
2. Mācību priekšmeta uzdevums ir radīt izglītojamajam iespēju:
2.1. veidot prasmi saskatīt un klasificēt fizikālās parādības dabā un tehnikā;
2.2. veidot zināšanas par fizikālajām parādībām, likumsakarībām un modeļiem;
2.3. veidot prasmi veikt fizikālu eksperimentu atbilstoši priekšrakstam;
2.4. veidot iemaņas iegūto zināšanu izmantošanā praktisku uzdevumu risināšanai;
2.5. veidot prasmi attēlot procesu grafikus, diagrammas un tabulas;
2.6. veidot radoša un racionāla darba iemaņas;
2.7. veidot vispārīgās pētnieciskā darba prasmes (analizēt, sistematizēt, secināt,
salīdzināt, klasificēt, modelēt);
2.8. veidot prasmi patstāvīgi plānot un organizēt dabaszinātņu pētījumu, izmantojot
novērošanas un eksperimenta metodes.
Mācību metodes
1. lekciju metode;
2. diskusiju metode (apgūstot jaunas prasmes un iemaņas),
3. grupu darbs,
4. problēmas izvirzīšana,
5. skolotāja skaidrojums,
6. atbilstošs skolēnu praktiskais darbs, apgūstot teorētisko kursu,
7. fizikālo pamatprasmju un iemaņu nostiprināšana un treniņš,
8. praktiska satura uzdevumu risināšana,
9. pētnieciskais darbs,
10. laboratorijas un praktikuma darbu izpilde,
11. fizikālo parādību vizuālā demonstrāciju metode.
(20% no kopējā stundu skaita fizikā) – Mehānika
|
|
|
|
Izmaiņas/dife-rencētā pieeja |
|
|
|
|
|
|
|
|
|
|
1. |
Ievadstunda. Darba drošības noteikumi fizikas kabinetā. SI sistēma. Mērījumi. Ķermeņi, masas punkts. |
1 |
|
|
Pielikumi (239.- 243.lpp.). 1.1.§. (MG). |
|
2. |
Vektori. Ķermeņu kustība. Atskaites sistēma/ķermeņi. Trajektorija, ceļš, pārvietojums. Uzdevumu risin. piemēri. |
2 |
|
Kārtējais vērtējums. Uzd.no MG; 1.1.-1.5. Ievadvērtējums. |
Pielikums -10.2.§ (244.-247.lpp.). |
|
3. |
Ātrums. Vienmērīga taisnlīnijas kustība. |
1 |
|
Kārtējais vērtējums. |
1.3.§, 1.4.§ (MG). |
|
4. |
Paātrinājums. Paātrināta taisnlīnijas kustība. Uzdevumi. |
2 |
1. pārb.d. |
Kārtējais vērtējums. |
1.5.§. 1.6.§ (MG). |
|
5. |
Vienkāršāko kustību grafiskais attēlojums. Kustība pa riņķa līniju. Uzdevumi. Kustība vizuālajā mākslā. |
2 |
|
Kārtējais vērtējums. |
1.7.§. 1.8..§ (MG). |
|
6. |
Terminu skaidrojums. Kontroluzdevumi, jeb pētnieciskais darbs. |
1 |
|
Robežvērtējums. |
MG - (30.-36.lpp.). |
|
7. |
Papildmateriāls – ķermeņu masa un blīvums. Ķermeņa inerce. |
1 |
|
Iegūto zināšanu un praktisko iemaņu vērtējums. |
Karjeras izvēle: fiziķis eksperimentātors, laborants. |
|
8. |
Spēku veidi.Uzd. risin. un piemēri. |
1 |
|
Kārtējais vērtējums. |
2.1., 2.2. § (MG). |
|
9. |
Darbība un pretdarbība. Reakcijas spēks un reaktīvā kustība. 3.Ņūtona likums. Uzd. risin. un piemēri. |
1 |
|
Kārtējais vērtējums. |
2.3., 2.4. § (MG). |
|
10. |
Deformāciju veidi.Miera stāvokļa berze. Slīdes berze, berzes koeficients. Huka likums. Piemēri. |
1 |
|
Kārtējais vērtējums. |
2.5., 2.6., 2.7. § no MG. |
|
11. |
Uzdevumu risināšanas piemēri, jeb pētnieciskais darbs. |
1 |
|
Kārtējais vērtējums. |
2.8., 2.9. § no MG. |
|
12. |
Svarīgāko terminu apkopojums un skaidrojums. |
1 |
|
Robežvērtējums. |
|
|
13. |
Vispasaules gravitācijas likums. Gravitācijas lauks. Smaguma spēks. Brīvās krišanas paātrinājums. Keplera likumi. |
1 |
Referāti, esejas, prezentācijas. |
Kārtējais vērtējums. |
3.1., 3.2., 3.3. § no MG. |
|
14. |
Ķermeņu kustība gravitācijas laukā. Vertikāls sviediens. Vertikāla krišana. Uzdevumu piemēri un to risinājumi. |
1 |
|
Uzd. no MG – (87. – 89. lpp.). |
4.1., 4.2. § no MG. |
|
15. |
Horizontāls sviediens. Slīps sviediens. Dabisko un mākslīgo pavadoņu (ZMP) kustība (no MG – 106. lpp.).Uzdevumi. |
1 |
|
Kārtējais vērtējums. |
4.3., 4.4. § no MG. |
|
16. |
Enerģija un darbs. Spēka darbs ķermeņa kustībā. Kinētiskā enerģija. Deformēta ķermeņa potenciālā enerģija. Virs zemes pacelta ķermeņa potenciālā enerģija. Uzdevumu piemēri un risinājumi. |
2 |
|
Kārtējais vērtējums. |
5.1., 5.2. § - MG. |
|
17. |
Pilnā mehāniskā enerģija. Mašīnu jauda un lietderības koeficients. |
1 |
Referāts – ”Iekšdedzes dzinēji, to attīstība un veidi”, jeb ”Iekšdedzes dzinēji mūsdienās”. |
Kārtējais vērtējums. |
5.6., 5.7. § - MG. |
|
18. |
Kermeņu sadursmes. Spēka impulss. Spēka moments. Uzdevumi. |
1 |
|
Kārtējais vērtējums. |
6.3., 6.4. § - MG. |
|
19. |
Vienkārši mehānismi. Statikas elementi. Uzdevumi. |
1 |
|
Kārtējais vērtējums. |
6.5., 6.6. § - MG. |
|
20. |
Mehāniskās svārstības. Par svārsta pulksteni. Brīvas nerimstošas svārstības. Atsperes svārsts. Atsaitē iekārta ķermeņa svārstības. Diega svārsts. |
1 |
Referāts-prezentācija „Fuko svārsts”. |
Kārtējais vērtējums. |
7.1., 7.2., 7.3. § - MG. |
|
21. |
Viļņu veidi, to fizikālās parādības, avoti. Stīgas svārstības. Skaņas viļņi. Skaņas izplatīšanās. Viļņu atstarošanās un lūšana. Piemēri. |
1 |
|
Kārtējais vērtējums. |
8.1., 8.2., 8.3., 8.5. § - MG. |
|
22. |
Gaisā un ūdenī. Atmosfēras spiediens. |
1 |
|
Robežvērtējums. |
UK – (110. – 111.lpp.). |
|
23. |
Hidrostatiskais spiediens šķidrumā. Šķidruma un gāzes plūsma. Šķidruma un gāzes plūsmas ātrums. Spiediens šķidruma un gāzes plūsmā. |
1 |
|
Kārtējais vērtējums. Uzd. no MG – (9.1. – 9.10.). |
9.2., 9.3., 9.4., 9.5. § - MG. |
|
24. |
Šķidruma virsmas spraigums. Slapināšana. Kapilārās parādības. Šķidruma un gāzes viskozitāte. Pretestības spēks. Cēlējspēks šķidrumā un gāzē. |
1 |
|
Kārtējais vērtējums. |
9.6., 9.7., 9.8., 9.9. § - MG. |
|
25. |
Mehānikas nodaļas noslēgums – terminu skaidrojums. |
1 |
|
Robežvērtējums un zināšanu un praktisko iemaņu vērtējums. |
|
|
|
Mācību literatūra |
||||
![]()
5.nod. Ieteicamais pamatzināšanu programmas saturs fizikā mehānikas sadaļai profesionālajā izglītībā 20% no kopējā stundu skaita fizikā
• Materiāls punkts. Atskaites sistēmas/ķermeņi. Trajektorija. Ceļš un pārvietojums. Vienmērīga taisnlīnijas kustība.
• Ātrums. Ātruma vienības. Kustības grafiskā attēlošana (grafiks, kas parāda ķermeņa koordinātas atkarībā no laika, un ātruma grafiks). Kustības relativitāte. Ātrumu saskaitīšana. Vienmērīgi paātrināta kustība. Momentānais ātrums.
• Paātrinājums. Paātrinājuma vienība. Ātruma grafiks vienmērīgi paātrinātai kustībai ar sākuma ātrumu. Ķermeņa brīvā krišana. Brīvās krišanas paātrinājums.
• Vienmērīga kustība pa riņķa līniju. Lineārais ātrums un leņķiskais ātrums. Sakarība starp šiem ātrumiem. Leņķiskā ātruma vienība. Paātrinājums vienmērīgā kustībā pa riņķa līniju (centrtieces paātrinājums). ZMP.
• Pirmais Ņūtona likums. Masa. Masas vienība. Blīvums. Blīvuma vienība.
• Spēks. Otrais Ņūtona likums. Spēka vienības
• Trešais Ņūtona likums.
• Vispasaules gravitācijas likums. Gravitācijas konstante. Smaguma spēks.
• Elastības spēki. Huka likums.
• Berzes spēks. Berzes koeficients.
• Impulss (kustības daudzums). Impulsa (kustības daudzuma) nezūdamības likums.
• Mehāniskais darbs. Jauda. Enerģija. Kinētiskā un potenciālā enerģija. Enerģijas nezūdamības likums mehānikā. Darba, jaudas un enerģijas vienības.
• Spēku saskaitīšana. Spēka moments. Ķermeņu līdzsvara nosacījumi. Svira.
Šķidrumu un gāzu mehāniskā kustība un īpašības
• Šķidrumu un gāzu fizikālās īpašības. Šķidrumu un gāzu spiediens. Paskāla likums. Spiediena vienības.
• Aerodinamika. Arhimēda cēlējspēks. Ķermeņu peldēšanas nosacījumi.
• Ūdens plūsma caur caurulēm. Virsmas spraigums.
Svārstības un viļņi
• Harmoniskas svārstības. Svārstību periods un frekvence. Frekvences vienība. Matemātiskā svārsta svārstību periods (bez izrisinājuma). Rezonanse.
• Šķērsviļņi un garenviļņi. Viļņa ātrums. Viļņa garums. Sakarība starp viļņa garumu, izplatīšanās ātrumu un frekvenci (vai periodu).

Vispārizglītojošā e-fizika (VeF) vidējā profesionālajā izglītībā
Makropasaules fizika – MEHĀNIKA
Ievads: pasaule un cilvēks, telpa un laiks, spēks un enerģija
Pasaule ir daudzveidīgu parādību jeb mainīgu ķermeņu kopums, kurā cilvēks ir viens no šiem mainīgajiem ķermeņiem jeb parādībām. Cilvēks ir garīga jeb vārdiski domājoša dzīvā būtne, kuras apziņā īstenojas noteikts sajūtams reālās apkārtējās pasaules atveids.
Cilvēks apzina pasaules parādības laikā un telpā, raksturojot parādības kā mainīgos ķermeņus ar to atbilstošajiem stāvokļiem.
Cilvēks apzina pasauli ne tikai faktoloģiski, noskaidrojot kas, kad, kur un kā notiek, bet apzina arī pasaules parādību cēlonību jeb cēloņseku sakarības, cenšoties noskaidrot arī to, kāpēc tas, tad, tur un tā notiek.
Ķermeņi un to kustība - f i z i k a .
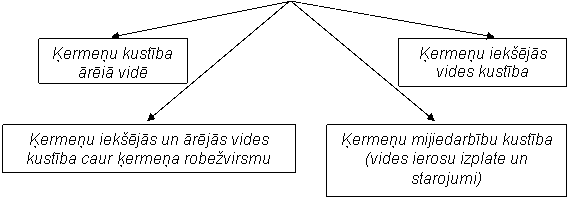
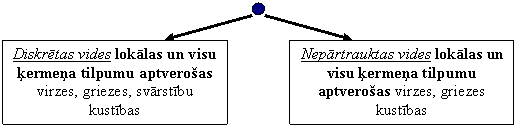
Katrs pasaules mainīgais ķermenis ir noteikts ar savu iekšējo un ārējo vidi, kuras var tikt apzinātas kā diskrētas vai nepārtrauktas, viendabīgas vai neviendabīgas, izotropas vai anizotropas vides. Ikviena vide ir noteiktu ķermeņu kopums, bet ikviens ķermeņis ir ārēji noformēta šo ķermeni veidojošā vide. Viss pastāv kopsaistībā - vieni ķermeņi un vides veido citus ķermeņus un vides.
FIZIKA ir fundamentāla zinātniska teorija (cilvēces uzkrāta specifiska dzīves pieredze) par materiālās pasaules ķermeņu telpisko stāvokļu mainību laikā un telpā jeb
M e h ā n i k a
Mehānika ir fizikas centrālā un vispārīgā daļa -
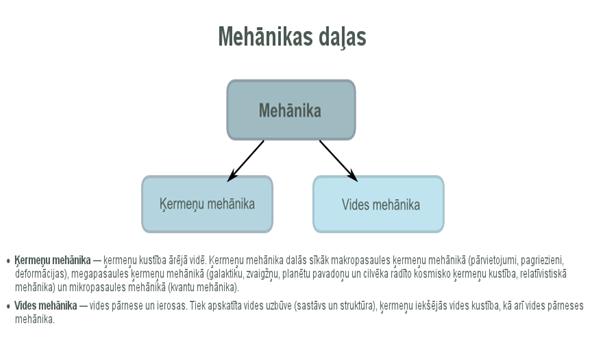
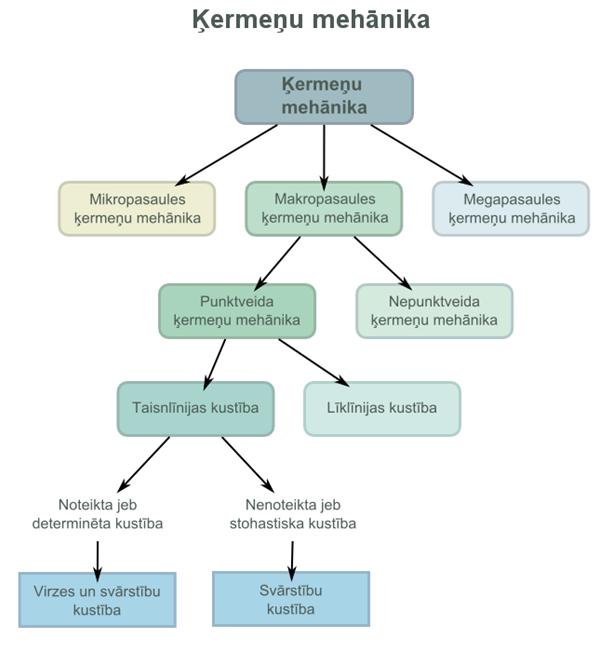
6.1. MAKROPASAULES ĶERMEŅU MEHĀNIKA
6.1.1.
6.1.2.
stohastiskas - gadījumrakstura virzes un svārstību kustības)
6.1.3.
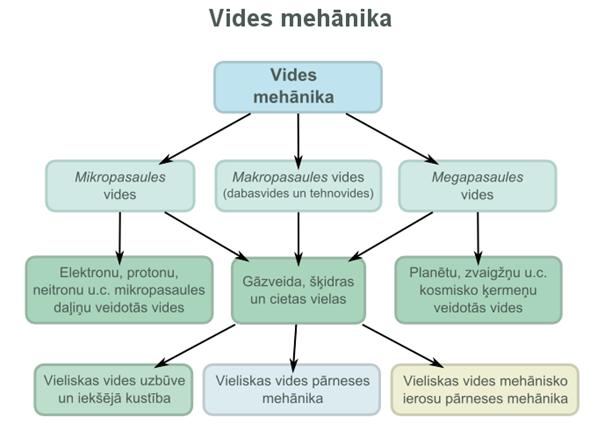
6.2. MAKROPASAULES ĶERMEŅU
(ķermeņu iekšējās vides pārvērtības, vides un vides ierosu pārnese)
6.2.1.
6.2.2
6.2.3
●
● Vides ierosu

6.3.1.att.
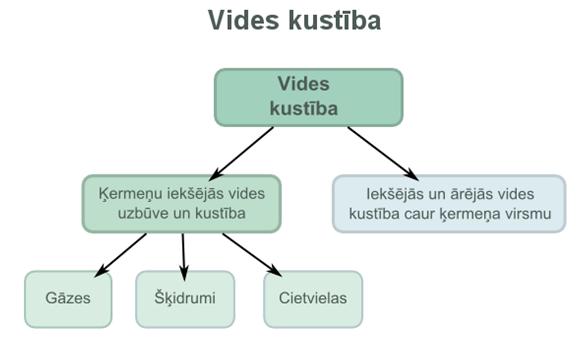
6.4. Ķermeņu iekšējās vides kustība ķermenī.
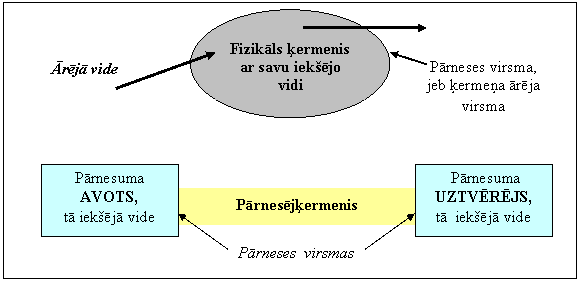
Iekšējās vides kustība ķermenī ir šo vidi veidojošo ķermeņu kustība.
6.6.
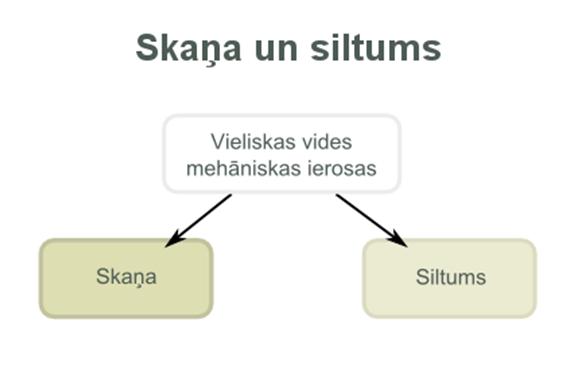
Lokāli ierosinot vidi - mainot vidi veidojošo ķermeņu savstarpējo novietojumu , šī vides izmaiņa visu to veidojošo ķermeņu kopsaistības dēļ izplatās arī pārējā vides aizņemtā telpā . Vides ierosa ir vides mainība, kas nav vides pārnese. Videi izmaiņa kā īslaicīgs vides ierosinājums jeb ierosa izplatās kā ierosas impulss, bet ilga ierosas uzturēšana rada nepārtrauktu ierosas izplatīšanos. Ierosas var būt ļoti dažāda rakstura, no kurām īpaši nozīmīga ir lokāli radītu vides harmonisko svārstību izplatīšanās viļņu veidā. Vides ierosas izplatīšanās ir būtiski atkarīga no konkrētās vides struktūras, kā arī no konkrētā ierosas veida un raksturlielumu vērtībām. Skaņas un siltuma izplates parādības ir tipiski vieliskas vides mehaniskās ierosas izplates piemēri.
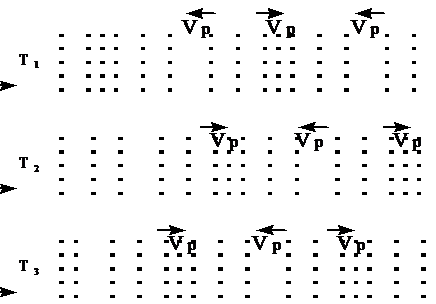

7.
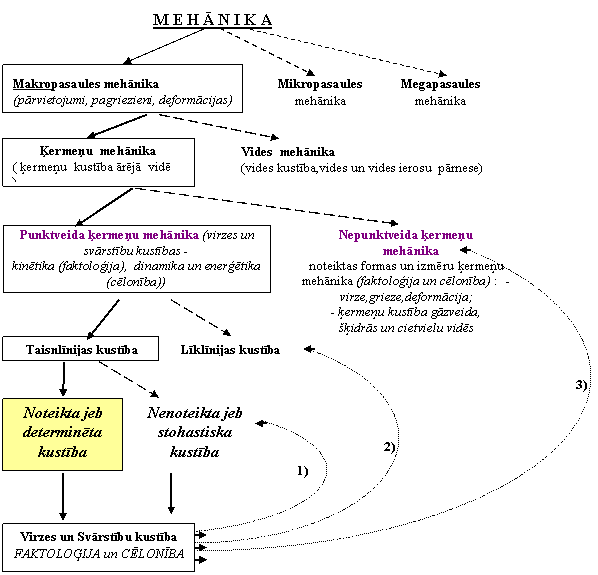
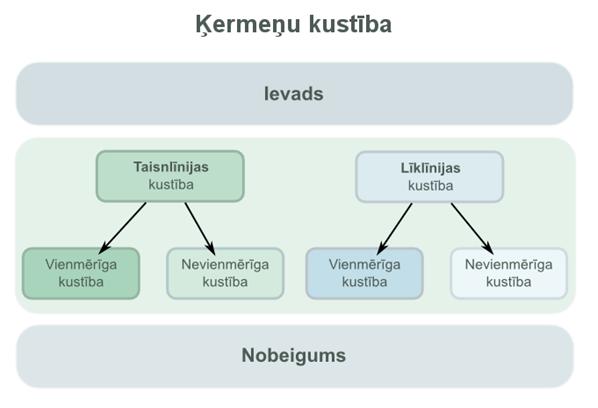
PUNKTVEIDA un NEPUNKTVEIDA ĶERMEŅU KUSTĪBU PAMATVEIDI
Ķermeņu kustību veidi
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ķermeņu kustību veidi
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8.nodaļa
Punktveida ķermeņu savstarpējā novietojuma un tā mainības principiālais apraksts
Punktveida ķermeņa jēdziens.
Īpašs gadījums ir viendabīgas iekšējās vides veidoti lodveida ķermeņi, kas ir uzskatāmi par punktveida ķermeņiem arī tuvumā, līdz pat šo ķermeņu saskarei.
Attāluma un virziena jēdzieni.
Punktveida ķermeņu savstarpējais novietojums raksturojas ar šo ķermeņu savstarpējiem attālumiem un virzieniem, kuros ap katru no tiem atrodas pārējie ķermeņi. Par ķermeņu savstarpējo novietojumu (attālumiem un virzieniem) ir jēga runāt, ja ir vismaz divi aplūkojamie ķermeņi.
Šajā sakarā lai atceramies ģeometrijas pirmsākumus pamatskolas matemātikā. Ar to tad arī jau sākas mehānikas parādību matemātiskais apraksts jeb matemātiskā modelēšana!
Atskaites sistēmas jēdziens.
Ķermeņu savstarpējā novietojuma apraksta izveide sākas ar
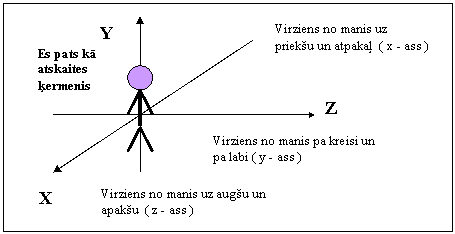
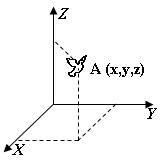
Ķermeņu telpiskā stāvokļa raksturlielums ir rādiusvektors (R vai r).
Ķermeņu telpisko stāvokļu kopums uzdod vienu no fizikālajām telpām - parasto mehānikas telpu. Saka, ka ķermeņi atrodas trīsdimensionālā telpā. Vienkāršākā gadījumā runā par divdimensionālu telpu jeb ķermeņu atrašanos plaknē. Visvienkāršākajā gadījumā ir viendimensionāla telpa, kad ķermeņi atrodas uz līnijas. Kāda telpa jāizvēlas ķermeņu savstarpējā novietojuma aprakstam, to nosaka šie ķermeņi un cilvēku ērtības un vienkāršības apsvērumi, izvēloties atbilstošu
Ķermeņi, to savstarpējais novietojums ir konkrēti - novērojami, kamēr telpa kā ķermeņu iespējamo atrašanās vietu kopums ir abstrakcija novērotā atveidei cilvēka apziņā.
Ikviena ķermeņa telpiskais stāvoklis ir zināms, ja zināmi trīs šī ķermeņa stavokļa raksturlielumi: rādiusvektora projekcijas
8.2.att.
9.nodaļa Fizikālu ķermeņu kustību daudzveidība
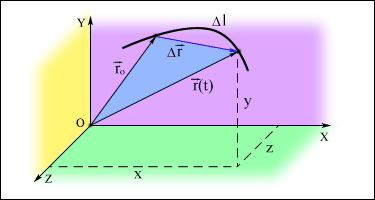
9.1. Vienkāršas taisnlīnijas virzes kustības
Ikviens ķermeņa pilnais pārvietojums - kustība sastāv no atsevišķiem to veidojošiem kustību soļiem, kuri telpā veido kustības trajektoriju jeb ceļu, bet laikā nosaka kustības ilgumu, kā arī raksturo kustības ātruma mainību. Kustības soļi laikā seko viens otram – īstenojas soļu virkne. Ikviens solis ir elementārkustība, kustības nedalāma daļa.
Līdz šim aplūkotās punktveida ķermeņa tainsnlīnijas virzes kustības
ir vienkāršas kustības.
9.2. Sarežģītas taisnlīnijas virzes kustības
Pasaule ir daudzveidīgu parādību kopums (ikviena parādība – mainīgs ķermenis, fizikālās parādības – daudzveidīgu ķermeņu daudzveidīgas kustības)
vx0(to) = const
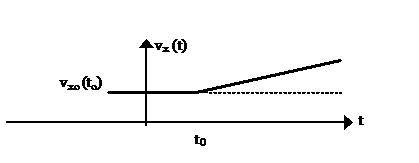
Šādai situācijai atbilst ikviena
(laikā secīgas jeb virknē īstenojošās kustības)
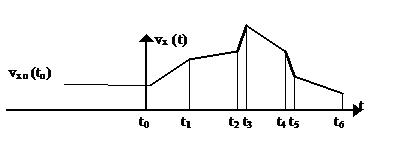
10. nodaļa KINĒTIKA
(
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pamatjēdzieni - spēks, darbs, enerģija
Dinamika
Spēks
Enerģika –
Enerģija
Spēka lauks -
(Vārds
Enrģijas lauks - telpa

10.2.att.
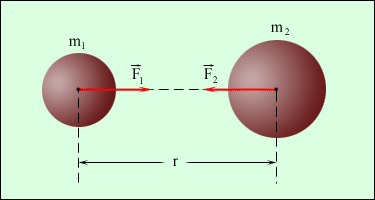
Gravitācija - ķermeņu savstarpēja pievilkšanās,
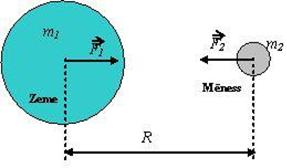
10.3.att. Gravitācijas spēks starp planētu Zeme un tās dabīgo pavadoni Mēnesi
Punktveida ķermeņu gravitācija ir izotropa - no virziena neatkarīga parādība
Dinamiku un enerģiku saista darba jēdziens (A = Fs; A = mgh).

, kur G = 6,67. 10-11 N.m2kg-2
10.4.att.
11. nodaļa Punktveida ķermeņa taisnlīnijas kustības
Ķermeņa
11.1.att. Pāra
12.nod. Ķermeņa kustības daudzums jeb ķermeņu impulss.
Dp
Dp
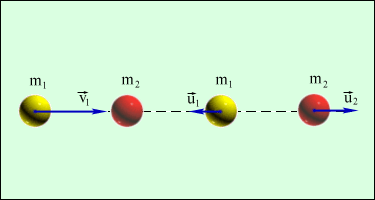
12.1.att.

12.2.att.
13.nod. Ķermeņu potenciālā un kinētiskā enerģija
Tādējādi ķermeņa
14.nodaļa Saistītu ķermeņu pāra izveides mehānika
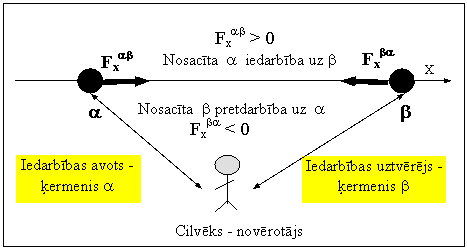
Divu punktveida ķermeņu jeb punktveida ķermeņu pāra
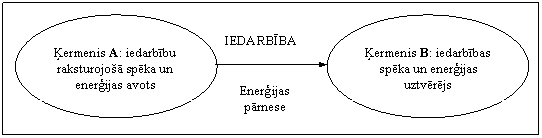
Taču arī šajā visvienkāršakajā situācijā kustības apraksts - matemātiskā modelēšana (faktoloģija un cēlonība) var būt formāli visai atšķirīga atkarībā no tā, kā izvēlētajā atskaites sistēmā savstarpēji novietoti aplūkojamie ķermeņi. Proti, formāli ir starpība, vai ķermenis B kā iedarbības uztvērējs atrodas koordinātu ass pozitīvā virzienā no iedarbības avota A vai arī ir novietots pretējā virzienā no tā (iedarbības avots - ķermenis A parasti tiek izvēlēts kā
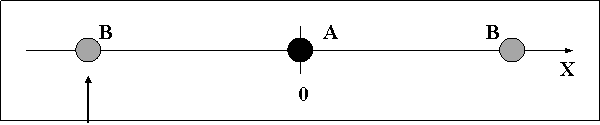
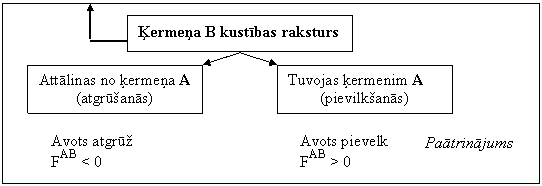
14.2.att.

15.nodaļa PUNKTVEIDA ĶERMEŅA SVĀRSTĪBU KUSTĪBA
Par svārstībām sauc kustības, kas raksturojas ar laikā secīgiem un telpā ierobežotiem stāvokļiem.
kur T - svārstību periods, Xa -
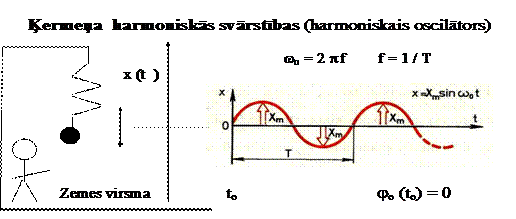
Harmoniskās svārstības īstenojas kā periodiska divu ķermeņu savstarpējā attāluma mainība, kuras cēlonis ir noteiktas dotā ķermeņu pāra mijiedarbības īstenojums. Šīs mijiedarbības specifika raksturojas ar to, ka ķermeņiem atrodoties periodiski mainīgā attālumā vienam no otra, tie vienmēr savstarpēji pievelkas (tuvojas) un atgrūžas (attālinās) ar spēku, kas proporcionāls attālumam līdz ķermeņu līdzsvara stāvoklim, ap kuru notiek svārstības.

15.2.att.
15.1. Sarežģītas svārstību kustības
Līdzīgi kā virzes kustības gadījumā, arī svārstību kustībā esošs ķermenis var vienlaicīgi īstenot vairākas vienkāršas jeb elementāras, dažādu iedarbības avotu rosinātas harmoniskas svārstības.
x (t) =
kur
Salīdzinoši vienkārša perodiska ķermeņa svārstību kustība ir tad, kad ķermenis vienlaicīgi veic harmoniskas svārstības divos dsavstarpēji perpendikulāros virzienos. Atkarībā no konkrētiem apstākļiem, kurus nosaka harmonisko svārstību frekvenču, amplitūdu un sākuma fāzu atšķirības, iegūstam raksturīgas
16.nodaļa STOHASTISKAS SVĀRSTĪBU
(gadījumrakstura jeb nenoteiktas ķermeņu kustības)
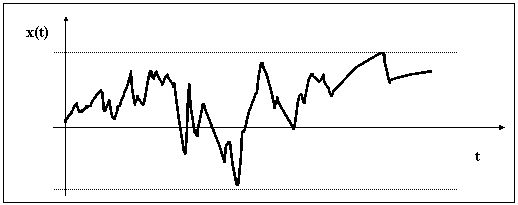
(vienkāršāko stohastisko - gadījumrakstura jeb varbūtejisko procesu matemātiskie aprakstu – modeļu veidošana)
Ja veicam stohastiska procesa raksturlieluma
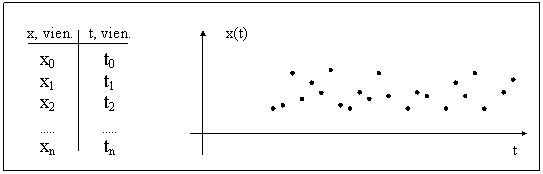
Stohastisku jeb gadījumrakstura procesu matemātiskie modeļi arī ir atbilstošas matemātiskās funkcijas. Tās sauc par
Stohastiskos procesus raksturojošās statistiskā sadalījuma funkcijas jeb, īsāk sakot, statistiskos
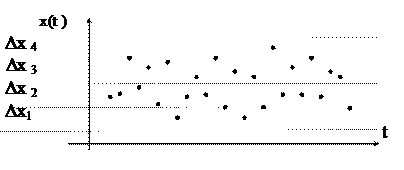
16.1.2.att.
Apzīmējot noteiktas vērtības atkārtojošos mērskaitļu skaitu attiecīgo mērskaitļu intervalā ar N , tiek iegūts atbilstošā stohastiskā procesa raksturojums - histogramma tabulas veidā. Pēc tam šo statistisko sadalījumu - histogrammu N (

![]()
Ļoti svarīgi ir saprast, ka jēga ir tikai histogrammas stabiņu augšējām horizontālajām svītriņām, kamēr vertikālajām līnijām histogrammās būtībā nav jēgas (tās lieto tikai grafika labākai uzskatāmībai).
Jo ilgāk un precīzāk veikti raksturlieluma
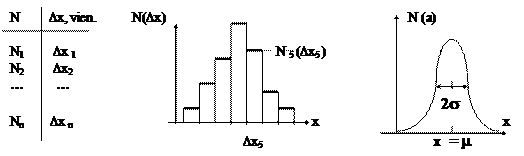
Stohastiskie procesi var tikt uzlūkoti arī kā stohastiskas svārstības - mainības stāvokļu gadījumrakstura svārstības ap kādu vidējo stāvokli.
Apzinot stohastiskos procesus mehānikā (iepazīstot punktveida ķermeņu gadījumrakstura kustību analīzi un sintēzi), mēs varam izdarīt ļoti nozīmīgu vispārinājumu - pārnest iegūtās atziņas arī vēl uz citu pasaules parādību zinātnisko apzināšanu!
Fizika ir fundamentāla zinātne ne tikai dabas un tehnikas jomā.
|
|
|
|
||||
|
Dinamika |
Enerģika |
|||||
|
|
v = 0 r(t)= const |
Fx = 0 |
Wpot = const |
|||
|
|
kustība |
|
Vienmērīga |
vx = const |
Fx = 0 |
Wkin = const |
|
Nevienmērīga |
vx |
|
Wkin ≠ const |
|||
|
|
Harmoniskas |
Atsperes svārsts |
Fx = - cx |
ΔWpot = = -ΔWkin |
||
|
Neharmoniskas |
Periodiskas Neperiodiskas Stohastiskas |
|
|
|||
|
kustība |
|
Skalāri vienmērīga |
Kustība pa riņķa līniju |
Centrtieces spēks |
Wkin = const |
|
|
Nevienmērīga |
|
|
|
|||
|
|
Harmoniskas |
Diega svārsts |
|
ΔWpot= -ΔWkin |
||
|
Neharmoniskas |
Roboti, kas īsteno atkārtojošās kustības |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K u s t ī b u p a m a t v e i d i |
|||
ĶERMEŅU MEHĀNIKA
(
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MAKROĶERMEŅU VIDES MEHĀNIKA
Makrovides mehānika - tā ir daudzu makroķermeņu makromehānika, kurā notiek šīs makrovides ierosu izplatīšanās (makroķermeņu kustību veidu mainība - pārveidošana: virzes - rotācijas kustību savstarpēja pārveidošana: kloķa-klaņa mehānisms, ritenis un tml.)