Riņķis un daudzstūris mākslā, dabaszinātnēs un matemātikā. Skolotāja atbalsta materiāls.

10. uzdevums.

Veicot uzdevumu, skolēni:

• veidos aprakstam atbilstošus zīmējumus;
• pamatos apgalvojumus, lietojot matemātisko valodu un simbolus;
• atkārtos zināmās sakarības riņķī;
• uzzinās sakarības par  hordas-pieskares leņķi, leņķi, ko veido divas hordas, divas sekantes ( divas pieskares);
• meklēs informāciju mācību literatūrā;
• veidos matemātiski korektus apgalvojumus.

 

Ieteikumi skolotājam.

• Var izvēlēties tikai dažus no piedāvātajiem apgalvojumiem, jo l) un m) piemēri ir skolēniem grūti saprotami un to rezultāts ir retāk lietojams.
• Uzdevumu var piedāvāt darbam grupās. Katra grupa pēta savus apgalvojumus un ar rezultātiem iepazīstina pārējos audzēkņus. Kopīgi veido un papildina formulu lapu.

 

Uzdevums.

Izveido katram piemēram atbilstošu zīmējumu un nosaki, kurš no apgalvojumiem ir patiess? Patiesos apgalvojumus pamato, bet aplamos pārveido tā, lai tie būtu patiesi! Pieraksti patiesos apgalvojumus savā formulu lapā! Ja nepieciešams, meklē informāciju mācību grāmatās!

a)      Riņķa līnijas diametrs, kas perpendikulārs pret hordu, dala šo hordu uz pusēm.

b)      Vienas un tās pašas riņķa līnijas divas vienādas hordas redzamas no centra vienādos leņķos.

c)      Jebkura horda savelk vienu riņķa līnijas loku.

d)     Visi ievilktie leņķi, kas balstās uz vienu un to pašu loku, ir vienādi.

e)      Ja divi ievilkti leņķi balstās uz kopēju hordu, bet dažādiem lokiem, tad to lielumu summa ir 180°.

f)       Ievilkts leņķis, kas balstās uz diametru, ir šaurs.

g)      Ievilkta leņķa lielums ir vienāds ar tāda centra leņķa lielumu, kas balstās uz tā paša loka, uz kura balstās ievilktais leņķis.

h)      Hordas pieskares leņķi veido no viena riņķa līnijas punkta novilkta horda un pieskare.

i)        Katra horda un pieskare veido vienu vienīgu hordas-pieskares leņķi.

j)        Hordas-pieskares leņķa ABC lielums vienāds ar tāda ievilkta leņķa lielumu, kas balstās uz tā paša loka, kuru ietver leņķis ABC.

k)      Divas hordas krustojoties veido 4 dažādus leņķus.

l)        Divu hordu veidotais leņķis BAE ir vienāds ar tādu loku leņķisko lielumu summas pusi, kurus ieslēdz atbilstošais krustleņķu pāris DAC un BAE (skat.zīm.).

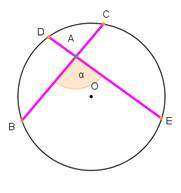
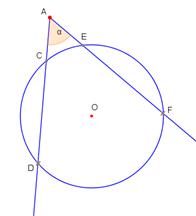
m) Leņķa DAF lielums, ko veido divas sekantes, ir vienāds ar tādu loku  un leņķisko lielumu starpības pusi, kuri atrodas starp šī leņķa malām (skat.zīm.).

 

11.uzdevums.

Veicot uzdevumu, skolēni:

• saskatīs sakarības ievilktiem un apvilktiem daudzstūriem;
• formulēs hipotēzi;
• pierādīs teorēmas par ievilktiem un apvilktiem daudzstūriem.

 

Ieteikumi skolotājam.

• Puse no skolēniem meklē sakarību ievilktiem daudzstūriem, otra puse – apvilktiem.
• Aicināt skolēnus mainīt attēlus un mērīt vajadzīgos lielumus. To var darīt gan , izmantojot datora rīkus (ActivInspire programmatūra), gan parasto lineālu.  Svarīgi, lai skolēni paši nonāk līdz hipotēzei.
• Pierādījumus veic skolēni kopā ar skolotāju.

 

 

Uzdevums.

Izmantojot Geonext failu T-8.5.gxt, noskaidrojiet, kāda sakarība ir spēkā visiem ievilktiem (apvilktiem) daudzstūriem.