Riņķis un daudzstūris mākslā, dabaszinātnēs un matemātikā. Skolotāja atbalsta materiāls.
| Site: | Profesionālajā izglītībā iesaistīto vispārizglītojošo mācību priekšmetu pedagogu kompetences paaugstināšana |
| Course: | MateT006 : Skolēnam atvērts matemātikas mācību process profesionālajā izglītībā |
| Book: | Riņķis un daudzstūris mākslā, dabaszinātnēs un matemātikā. Skolotāja atbalsta materiāls. |
| Printed by: | Guest user |
| Date: | Friday, 13 March 2026, 8:47 PM |
Description
Skolotājam izmantojamie materiāli - uzdevumi, darba lapas, vizuālie materiāli.
Table of contents
- Titullapa
- Tematiskais plānojums. Riņķis un daudzstūri.
- 1.stunda. Riņķi un daudzstūri – mākslas, dabaszinātņu un matemātikas objekti.
- 2.stunda. Četrstūru elementu aprēķināšana.
- 3.stunda. Četrstūru konstruēšana pēc dotajiem elementiem.
- 5.stunda. Atkalsatikšanās ar riņķi un tā elementiem.
- 4.stunda. Cik tālu mēs varam redzēt?
- 6.stunda. Teorēmas par riņķī ievilktu un ap riņķi apvilktu četrstūri.
- 7.stunda. Ievilktu un apvilktu daudzstūru elementu aprēķināšana.
Titullapa



Riņķis un daudzstūris mākslā, dabaszinātnēs un matemātikā. Skolotāja atbalsta materiāls
Materiāls izstrādāts
ESF Darbības programmas 2007. - 2013.gadam „Cilvēkresursi un nodarbinātība”
prioritātes 1.2. „Izglītība un prasmes”
pasākuma 1.2.1.„Profesionālās izglītības un vispārējo prasmju attīstība”
aktivitātes 1.2.1.2. „Vispārējo zināšanu un prasmju uzlabošana”
apakšaktivitātes 1.2.1.1.2. „Profesionālajā izglītībā iesaistīto pedagogu
kompetences paaugstināšana”
Latvijas Universitātes realizētā projekta
„Profesionālajā izglītībā iesaistīto vispārizglītojošo mācību priekšmetu pedagogu
kompetences paaugstināšana”
(Vienošanās Nr.2009/0274/1DP/1.2.1.1.2/09/IPIA/VIAA/003,
LU reģistrācijas Nr.ESS2009/88) īstenošanai.
Rīga, 2010.
Tematiskais plānojums. Riņķis un daudzstūri.
8
stundas
Tematiskais
plānojums
|
Temata satura bloks |
Stunda |
Tematā sasniedzamais rezultāts no MPP |
Stundas temats |
Stundā sasniedzamais rezultāts |
Atbalsta materiāli |
Mācību līdzekļi |
Komentāri un ieteikumi |
|
|
Uzd.nr. |
Citi AM |
|||||||
|
Daudzstūru elementu aprēķināšana |
1. |
Saskata un izmanto
trijstūru īpašības, sakarības starp trijstūra malām un leņķiem,
pamatojot sakarības starp
nogriežņiem un leņķiem daudzstūros, aprēķinot četrstūru un
regulāru daudzstūru elementus un laukumu. Veido aprakstam
atbilstošus daudzstūru zīmējumus, lietojot pieņemtos
apzīmējumus Saskata riņķa līnijas, riņķa un daudzstūru lietojumu mākslā, arhitektūrā un dabā. |
Riņķi un daudzstūri – mākslas, dabaszinātņu un matemātikas
objekti. |
Saskata riņķa līnijas, riņķa un daudzstūru lietojumu
mākslā, arhitektūrā un dabā. Izmanto IT informācijas
iegūšanai un prezentācijas veidošanai. Prezentē grupas darbu. |
1. |
|
Skolēni strādā datorklasē (vismaz 1 dators katrai
skolēnu grupai) |
Ierosmei stundu var iesākt ar filmu „Matemātika mākslā” http://www.youtube.com/watch?v=hhhhfqiJ7nU&feature=related Alternatīva – informāciju savāc, apkopo, izveido
prezentāciju mājās, klasē strādā ar 1 datoru un projektoru, demonstrējot
prezentāciju. |
|
2. |
Četrstūru elementu aprēķināšana. |
Izmanto sakarības trijstūrī, lai aprēķinātu
četrstūra elementus. Izmanto sakarības četrstūros, lai aprēķinātu to
elementus. |
2. 3. |
Geonext fails |
|
|
||
|
3. |
Četrstūru konstruēšana pēc dotajiem elementiem. |
Plāno uzdevuma risinājumu. Konstruē daudzstūrus, izmantojot četrstūru definīcijas, pazīmes vai
īpašības. |
4. 5. |
Geonext fails |
|
|
||
|
Leņķi riņķī |
4. |
Veido aprakstam
atbilstošus riņķa un ar riņķi saistīto nogriežņu un leņķu
zīmējumus, lietojot pieņemtos
apzīmējumus. Lieto jēdzienus – horda, pieskare, sekante, loks,
centra leņķis, ievilkts leņķis, riņķa
sektors, riņķa segments, hordas–pieskares
leņķis; leņķis, ko veido divas hordas;
leņķis, ko veido divas sekantes,
(pieskares), , veidojot zīmējumus un
risinot uzdevumus. Aprēķina
hordas–pieskares leņķi; leņķi, ko veido
divas hordas, divas sekantes, divas
pieskares. |
Cik tālu mēs varam redzēt? |
Atrisina praktisku problēmu par attālumu līdz horizontam. Sadarbojas, risinot problēmu. Izsaka idejas iegūtā rezultāta izmantošanai citās dzīves situācijās. |
6. |
Pētnieciskais darbs. |
|
Var izvēlēties arī objektus, kas tieši saistās ar
audzēkņu apskates objektiem, konkrētu situāciju skolā vai apkārtnē. |
|
5. |
Atkalsatikšanās ar riņķi un tā elementiem. |
Lieto ar riņķi saistītos jēdzienus. Nosaka centra leņķa un ievilkta leņķa lielumus. |
7. 8. 9 10.. |
Darba lapas skolēniem 2 varantos. Geonext faili. PowerPoint prezentācija 2., 3.slīds |
Interaktīvā tāfele |
Var aicināt mājās atkārtot pamatskolā mācītās
sakarības riņķi, patstāvīgi meklēt informāciju mācību grāmatās, izmantot atbalsta
materiāla prezentāciju. |
||
|
Ievilkti un apvilkti daudzstūri |
6. |
Saskata un izmanto
trijstūru īpašības, sakarības
starp trijstūra malām un leņķiem,
aprēķinot ievilktu un
apvilktu daudzstūru elementus, laukumu. Veido aprakstam
atbilstošus ievilktu un apvilktu daudzstūru
zīmējumus, lietojot pieņemtos
apzīmējumus. Lieto teorēmas par
riņķī ievilktu četrstūri un ap riņķi apvilktu četrstūri. Lieto jēdzienus –ievilkts četrstūris,
apvilkts četrstūris, rombs, paralelograms,
trapece, taisnstūris, regulārs sešstūris –, veidojot zīmējumus un risinot uzdevumus. |
Teorēmas par riņķī ievilktu un ap riņķi apvilktu
četrstūri. |
Izvirza hipotēzes
par ievilktu un apvilktu četrstūri, vērojot demonstrējumu. Pierāda teorēmas
par riņķī ievilktu četrstūri un ap riņķi apvilktu četrstūri. Lieto jēdzienus –ievilkts četrstūris,
apvilkts četrstūris Veido uzdevuma nosacījumiem atbilstošu zīmējumu. |
11. |
Geonext faili T-8.5. gxt PowerPoint prezentācija 4.-16.slīds |
Dators un projektors demonstrējumam |
Var izmantot arī dabaszinātņu un matemātikas
projektā izstrādātos vizuālos materiālus. |
|
7. |
Ievilktu un apvilktu daudzstūru elementu
aprēķināšana. |
Lieto teorēmas par
riņķī ievilktu četrstūri un ap riņķi apvilktu četrstūri. Plāno risinājuma
gaitu, saskatot un izmantojot trijstūru īpašības un sakarības starp trijstūra malām un leņķiem. Aprēķina ievilktu
un apvilktu daudzstūru elementus, laukumu. |
12. |
Geonext faili |
|
|
||
|
|
8. |
|
Nobeiguma pārbaudes darbs. |
|
|
|
|
Ieteikums izmantot projekta piedāvāto ND. |
1.stunda. Riņķi un daudzstūri – mākslas, dabaszinātņu un matemātikas objekti.
1.uzdevums.
Veicot uzdevumu,
skolēni:
- saskata
riņķa līnijas, riņķa un daudzstūru lietojumu mākslā, arhitektūrā un dabā;
- izmanto
IT informācijas iegūšanai un prezentācijas veidošanai;
- prezentē
savu darbu;
- veido
jautājumus par atbilstošo tematu.
Ieteikumi skolotājam.
- Tā kā skolēniem ir nepieciešamās priekšzināšanas par daudzstūriem un riņķiem no pamatskolas, viņi patstāvīgi var veidot prezentāciju. Temats - Riņķis un daudzstūris mākslā, dabaszinātnēs un matemātikā.
- Ierosmei
stundu var iesākt ar filmu „Matemātika mākslā”
- Skolēni sadalās grupās pa 3.Katrai grupai cits uzdevums.
- Uzdevumu grupām skolotājs demonstrē, izmantojot vizuālo materiālu.
- Klasē izveidosies kopīga prezentācija ar 18 slīdiem, kurus skolēni jau pirms stundas var sakārtot vienā prezentācijā un katra grupa komentē savus slīdus. (skolotājs, uzdodot uzdevumu var ar skolēniem vienoties par vienotu noformējumu – fontiem, fonu, stilu, tad darbs izskatīsies vēl viendabīgāks).
- Vērojot citas grupas prezentācijas, katram skolēnam iz jāuzraksta viens jautājums katrai grupai par atbilstošo tematu. Dažus no jautājumiem katrai grupai lūdz uzdot. Skolotājam būtu jāseko līdzi, lai katrs skolēns kādai grupai būtu uzdevis savu jautājumu.
- Stundas beigās skolotājs apkopo idejas no skolēnu stāstītā un veic kopsavilkumu, uzsvērdams, ka, lai veiksmīgi izmantotu riņķi un daudzstūri:
- jāuzzina vairāk īpašību un sakarību katrā no šīm figūrām;
- jāzina kopsakarības šīm figūrām;
- jāsaprot dažas likumsakarības, kas saista šīs figūras.
Tas arī ir temata galvenais uzdevums:
- izmantot zināšanas par trijstūri, lai labāk iepazītu daudzstūrus;
- iepazīt dažādus leņķus riņķī, lai varētu pētīt riņķa un daudzstūru savstarpējās likumsakarības.
Vizuālais materiāls
demonstrēšanai skolēniem
Riņķis un daudzstūris mākslā, dabaszinātnēs un matemātikā
Katrai grupai:
1) jāizveido Power Point prezentācijas 2 slīdus, atrodot, jūsuprāt, visraksturīgākos piemērus savam
uzdevumam.
1.grupa.
Riņķis mākslā.
2.grupa.
Riņķis dabaszinātnēs.
3.grupa.
Riņķis matemātikā.
4.grupa.
Daudzstūri mākslā.
5.grupa.
Daudzstūri dabaszinātnēs.
6.grupa.
Daudzstūri matemātikā.
2) jāsagatavo stāstījumu (apm.3 min.), atbildot uz
jautājumiem:
·
Kāpēc figūru
izmanto mākslā, dabaszinātnēs un matemātikā (dabas objektiem šāda forma, palīdz
uzskatāmi attēlot, piem., trigonometriskais riņķis, vizuāli skaisti, ekonomiski
izdevīgas formas, piem., regulārs sešstūris utt.). skolēniem jāmin konkrēti piemēri
un jāilustrē savs stāstījums.
·
Kas būtu svarīgi
uzzināt par doto figūru, lai varētu to efektīvi izmantot praksē, sadzīvē,
zinātnē, mākslā, būvniecībā ...
2.stunda. Četrstūru elementu aprēķināšana.
2.uzdevums.
Veicot uzdevumu,
skolēni:
- atkārtos četrstūru veidus;
- izveidos dažādu četrstūru modeļus, izmantojot to galvenās pazīmes.
Ieteikumi skolotājam.
- Uzdevumu var piedāvāt veikt pāros. Tas attīstītu sadarbības prasmes, kā arī skolēni viens otram palīdzētu atcerēties dažādo četrstūru veidus un pazīmes.
- Var skolēniem piedāvāt jau sadalītu kvadrātu. Viņi var praktisko darbu nodarbībās izveidot šādus kvadrātus no plastikāta, koka u.c.materiāliem.
- Stundas gaitā piedāvājiet atrisināt vēl citus aprēķina uzdevumus, kuros jāizmanto pamatskolā apgūtās zināšanas par daudzstūriem vai sakarības trijstūros.
Uzdevums.
Sagrieziet kvadrātu tādās daļās, kā parādīts zīmējumā. Daļas sajauciet un pēc tam izveidojiet:
a) tādu pašu kvadrātu;
b) taisnleņķa vienādsānu trijstūri;
c) taisnstūri, kas nav kvadrāts;
d) paralelogramu, kas nav taisnstūris;
e) trapeci.
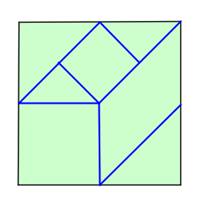
3.uzdevums.
Veicot uzdevumu,
skolēni:
- skolēni izmantos sakarību taisnleņķa trijstūrī, aprēķinot kvadrāta elementus;
- risinās kvadrātvienādojumu un izvērtēs tā saknes atbilstoši uzdevuma nosacījumiem;
- veiks skaitļa noapaļošanu.
Uzdevums.
1.kursa audzēkne Gita izveidoja kvadrātveida torti, kuras diagonāles garums iznāca par 15cm garāks nekā tortes malas garums. Gitai ir mācīts, ka 5 cm2 tortes noklāšanai ar krēmu, nepieciešams saputot 70g saldā krējuma. Cik gramu saldā krējuma Gitai nepieciešams saputot šai tortei?
3.stunda. Četrstūru konstruēšana pēc dotajiem elementiem.
4.uzdevums.
Veicot uzdevumu, skolēni:
- mācīsies plānot uzdevuma risinājuma gaitu;
- atkārtos par leņķiem un to īpašībām;
- izmantos trijstūru līdzību uzdevumos par četrstūriem;
- uzziņas literatūrā noskaidros Talesa teorēmas būtību;
- attīstīs matemātisko valodu.
Ieteikumi skolotājam.
- Risinājumu piedāvā uz atsevišķām kartiņām, lai skolēni tās secīgi sakārto.
- Kopīgi ar skolēniem jāpārrunā katrs risinājuma solis, aicinot viņus izstāstīt risinājumu.
- Var piedāvāt skolēniem pēc apraksta veidot zīmējumu pašiem.
Uzdevums.
3.kursa audzēknis Kārlis devās uz matemātikas stundu, kurai bija sagatavojis uzdevuma par trapeci atrisinājumu. Uzdevums bija grūts un atrisinājums garš, tāpēc Kārlis to bija sarakstījis pa soļiem uz mazām lapiņām, aizmirsdams tās sanumurēt pēc kārtas. Kārlis bija lepns par paveikto līdz brīdim, kad klasē sacēlās caurvējš un visas risinājuma lapiņas aizpūta pa klasi. Palīdzēsim Kārlim sakārtot risinājumu!
Kārļa risinātais uzdevums.
Dota trapece, kuras malas AB║CD un malas AB garums ir 3 reizes lielāks nekā malai CD (skat.zīm.). Malas AB viduspunkts F ir savienots ar trapeces virsotnēm C un D. Malas CD viduspunkts E ir savienots ar trapeces virsotnēm A un B. Nogriežņi AE un DF krustojas punktā M, nogriežņi BE un FC krustojas punktā N. Aprēķināt nogriežņa MN garumu, ja malas AB garums ir a.
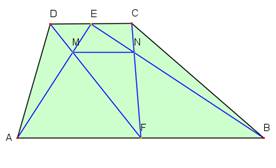
Lapiņas sagriešanai.
Risinājuma plāna punkti uz lapiņām. Sakārtojiet lapiņas (sanumurējiet) pareizajā secībā!
AB = a, tad AF = FB = DC = Aplūkosim ∆FNB un ∆CNE. FB║CE, FC un BE krustojas, tātad Līdz ar to ∆FNB~∆CNE
![]()
![]() , tad DE = EC =
, tad DE = EC = ![]()
![]() BFC =
BFC = ![]() FCE un
FCE un ![]() FBE =
FBE = ![]() BEC (iekšējie
šķērsleņķi).
BEC (iekšējie
šķērsleņķi).
Aplūkosim ∆AEB. AB║MN, tāpēc ∆AEB~ ∆MEN un Tā kā Savukārt, Ievietojot zināmos lielumus, iegūst ∆AMF~ ∆EMD, tātad ∆FNB~∆CNE, tātad
![]() .
.![]() , tad
, tad ![]() .
.![]()
![]() jeb
jeb ![]()
![]()
![]()
Aplūkosim No iepriekšējām sakarībām seko, ka Tad pēc Talesa teorēmas: AB║MN. Aplūkosim ∆AMF un ∆EMD. AF║DE, AE un FD krustojas, tātad Līdz ar to ∆AMF~∆EMD
![]() AEB.
AEB.![]()
![]() EAF =
EAF = ![]() AED un
AED un ![]() AFD =
AFD = ![]() FDE (iekšējie
šķērsleņķi).
FDE (iekšējie
šķērsleņķi).
5.uzdevums.
Veicot uzdevumu, skolēni:
- Konstruē rombu, ja dota diagonāle un augstums.
Ieteikumi skolotājam.
- Stundas gaitā var piedāvāt vēl citus uzdevumus konstruēt daudzstūrus.
- Dažos uzdevumos var skolēniem lūgt izveidot tikai konstrukcijas plānu.
- Var piedāvāt skolēniem izveidot arī dekora skici, ievērojot atbilstošus sienas izmērus un mērogu.
Uzdevums.
Celtniecības koledžas audzēkņi gribēja savai skolai atstāt dāvanu – pašu zīmētu sienas dekoru. Lai tas piestāvētu pārējai telpai, viņi nolēma, ka dekors jāveido romba formā. Skolēni izmērīja šī romba augstumu un diagonāli. Kā viņiem uzkonstruēt pašu rombu?
5.stunda. Atkalsatikšanās ar riņķi un tā elementiem.
7.uzdevums.
Veicot uzdevumu, skolēni:
- atkārtos sakarības par ievilktu un centra leņķi;
- sadarbosies, strādājot viena varianta grupās;
- attīstīs matemātisko valodu, stāstos otram skolēnam savus risinājumus.
Ieteikumi skolotājam.
- Skolēni atkārto no pamatskolas par ievilktu un centra leņķi.
- Darba lapas 2 variantos. Pēc to aizpildīšanas, var izveidot vairākas 3 – 4 skolēnus grupas, kuriem bija 1.variants, un vairākas - 2.varianta. Skolēni šajās grupās salīdzina rezultātus 1.-5.uzdevumam, pārrunā atšķirības un nonāk līdz pareizam rezultātam. Tad skolēni apvienojas pāros, lai katrs būtu no sava varianta un izstāsta savus uzdevumu risinājumus otram skolēnam.
- Skolotājs var ievākt darba lapas, lai pārliecinātos par katra paša izveidoto uzdevumu atbilstību nosacījumiem. Tas dotu iespēju arī skolotājam pārliecināties par katra skolēna izpratni par ievilktu un centra leņķi.
- Nākamo stundu var iesākt, aktualizējot vēlreiz jautājumu par leņķiem riņķī un piedāvājot katram izpildīt divus cita skolēna izveidotos uzdevumus.
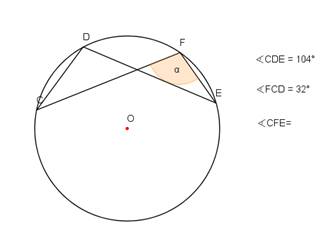
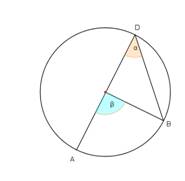
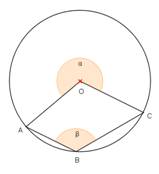
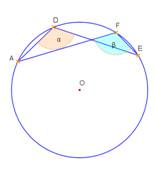
Darba lapa skolēnam
1.variants
Uzdevums.
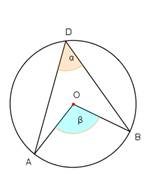
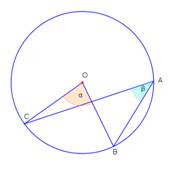
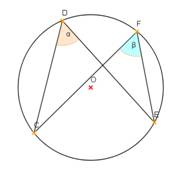
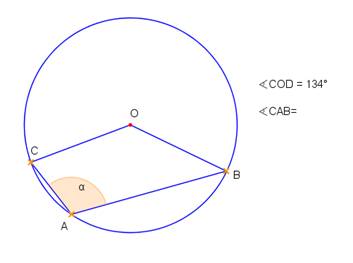
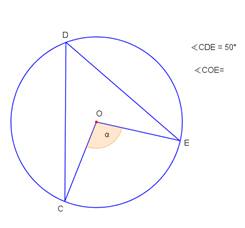
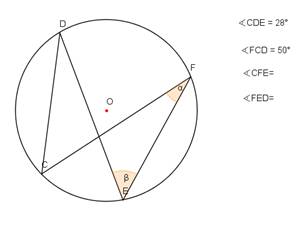
- Noteikt sakarību starp leņķiem α un β 1. – 3. zīmējumā!
- Noteikt leņķu lielumus 4. – 5.zīmējumā!
- Izveidojiet divus savus uzdevumus, kuros būtu nepieciešams noteikt centra leņķus un ievilktus leņķus! Izveidojiet atbilstošus zīmējumus (6., 7.)!
Lenķi un riņķis
|
|
|
|
|
1.
|
2. |
3. |
|
|
|
|
4.
|
5. |
|
|
|
|
6.
|
7.
|
Darba lapa skolēnam
2.variants
Uzdevums.
- Noteikt sakarību starp leņķiem α un β 1. – 3. zīmējumā!
- Noteikt leņķu lielumus 4. – 5.zīmējumā!
- Izveidojiet divus savus uzdevumus, kuros būtu nepieciešams noteikt centra leņķus un ievilktus leņķus! Izveidojiet atbilstošus zīmējumus (6., 7.)!
Lenķi un riņķis
|
|
|
|
|
1.
|
2. |
3. |
|
|
|
|
4.
|
5. |
|
|
|
|
6.
|
7.
|
8.uzdevums.
Veicot uzdevumu, skolēni:
- veidos aprakstam atbilstošu zīmējumu
- veiks loģiskus spriedumus, izmantojot sakarības trijstūros un par leņķiem riņķī;
- paskaidros katru darbību ar matemātiskiem pamatojumiem.
Ieteikumi skolotājam.
- Aicināt skolēnus veikt pēc apraksta pierādījumu, pa soļiem veidojot arī zīmējumu un pierakstot pamatojumu, vai un kāpēc tā drīkst darīt.. Tas varētu skolēnus veiksmīgāk atrast kļūdu.
- Vajadzētu īpaši uzslavēt skolēnus, kuri atrod kļūdu, jo pašam izdarīt pareizi ir vienkāršāk nekā atrast kļūdu cita risinājumā.
Uzdevums.
Kāds 1.kursa audzēknis, kurš tikko sācis mācīties tematu par riņķi un ar to saistītajiem nogriežņiem, ierodas nākamajā matemātikas stundā un svinīgi paziņo, ka viņš nepiekrīt skolotāja iepriekšējās stundas stāstījumam par hordu un diametru, jo viņš, lūk, pierādīja pavisam ko citu. Un tā viņa apgalvojums un pierādījums ir šāds.
Horda, kas neiet caur riņķa līnijas centru ir vienāda ar šī riņķa diametru!
Pierādījums.
1) Novelkam riņķa līnijas diametru AB.
2) Caur punktu B novelkam hordu BC, kas neiet caur riņķa līnijas centru.
3) Caur hordas BC viduspunktu D un punktu A novelkam jaunu hordu AE.
4) Savienojam ar nogriezni punktus E un C.
5) Apskatām trijstūrus ABD un EDC.
Pēc konstrukcijas BD = DC.
![]() .
.
![]()
Ja viena trijstūra mala un divi leņķi ir vienādi ar otra trijstūra malu un diviem leņķiem, tad šie trijstūri ir savstarpēji vienādi.
Tātad ∆BDA=∆EDC. No tā varam secināt, ka AB = EC, tātad jebkura horda riņķī ir vienādā garumā ar diametru.
Kur skolēns kļūdījās? Izveido aprakstam atbilstošu zīmējumu, paskaidro, kur viņš kļūdījās un izlabo kļūdu viņa apgalvojumā!
9.uzdevums.
Veicot uzdevumu, skolēni:
- saskata zīmējumā ievilktus leņķus;
- lieto zināšanas par ievilktiem leņķiem, kas balstās uz diametru.
Ieteikumi skolotājam.
- Var izmantot materiālā piedāvāto Geonext failu un izveidot skolēniem individuālus zīmējumus, saglabājot ideju par ievilktiem leņķiem, kas balstās uz diametru.
- Var demonstrēt attēlu uz interaktīvās tāfeles, parādot dažādus novietojumus, uzsverot ka kādi no leņķiem visās situācijās saglabājas taisni.
Uzdevums.
Attēlā dots riņķis ar centru O un vairāki leņķi.
- Kuri riņķī iezīmētie leņķi ir taisni?
- Atzīmējiet tos, lietojot atbilstošu simboliku!
- Pamatojiet, kāpēc jūsu iezīmētie leņķi ir taisni!
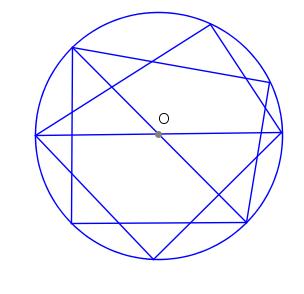
4.stunda. Cik tālu mēs varam redzēt?
6.uzdevums.
Veicot uzdevumu, skolēni:
- patstāvīgi pētīs praktisku problēmu par attālumu līdz horizontam;
- sadarbosies problēmas atrisināšanai;
- izteiks idejas iegūtā rezultāta izmantošanai citās dzīves situācijās.
Ieteikumi skolotājam
- Rosināt skolēnus izteikt savas idejas, kā šo problēmu risināt.
- Kopīgi ar skolēniem nonākt pie secinājuma, ka, lai atrisinātu šo konkrēto problēmu, teorētiski jānoskaidro, cik tālu ir horizonts. Horizonta līniju mēs nevar sasniegt: jo tālāk ejam, jo tā arvien attālinās, tomēr horizonts nav mirāža, tā reāli eksistē. Kopīgi ar skolēniem, ja nav citu racionālu ideju vai risinājuma piedāvājumu, izveidojiet shematisku zīmējumu (skat.zīm.).
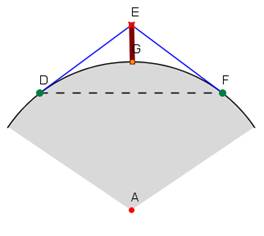
- Aiciniet pāros skolēnus aprēķināt attālumu līdz horizontam ED (EF). Varat piedāvāt papildus informāciju: Zemes rādiuss ir apm.6400km; varat ļaut pašiem meklēt nepieciešamo informāciju.
- Atkarībā no skolēnu spējām un laika, var problēmu risināt vispārīgajam gadījumam, tikai pēc tam ielikt konkrētus lielumus, bet var piedāvāt risināt arī tikai konkrēto problēmu. Vispārīgajā gadījumā attālums līdz horizontam ir aprēķināms pēc formulas:
![]() , kur EF – attālums līdz horizontam,
, kur EF – attālums līdz horizontam,
R – Zemes rādiuss (AD),
h – novērotāja acs augstums virs zemes (EG).
- Stundas beigās katrs pāris izsaka savas domas par iespēju redzēt Zilo kalnu un īsi to pamato. Būtu jārosina izteikt gan teorētisko iespēju, gan citus apstākļus, kas var traucēt redzamību. Atkarībā no atmosfēras refrakcijas, t.i., gaismas staru izkliedes atmosfērā, horizonta attālums var mainīties pat 6% robežās no teorētiski aprēķinātā. Attālums līdz horizontam samazinās, ja ir zems gaisa spiediens, silts, sauss laiks, dienā sliktāka redzamība nekā no rīta vai vakarā, virs sauszemes redzamība mazāka nekā virs jūras.
- Var piedāvāt pētījumu turpināt un noskaidrot, kā ir ar teorētisku iespēju redzēt Rīgas Pētergaili.
Darba lapa skolēnam
Cik tālu mēs varam redzēt?
Pētnieciskais uzdevums.
Situācijas apraksts.
1.kursa audzēkņi devās uz Rīgu mācību ekskursijā un viens no apskates objektiem ekskursijas laikā bija Cēsu Svētā Jāņa baznīca. Gatavojoties ekskursijai, skolēni apkopoja informāciju par apskates objektiem, un Montas uzdevums bija pārējiem pastāstīt par šo baznīcu. Monta atrada sekojošu informāciju.
„Cēsu Svētā Jāņa baznīca ir lielākā viduslaiku bazilika ārpus Rīgas. Baznīca ir 65 m gara un 32 m plata trīsjomu bazilika, ko rietumu galā ievada masīvais 65 m augstais zvanu tornis ar 15 m augstu gotisku smaili. ...Baznīca jau kopš 19.gadsimta pirmās puses pievērsusi uzmanību kā vēstures un arhitektūras piemineklis. ... Baznīcas slieksnis atrodas tieši 100 metrus virs jūras līmeņa. No baznīcas torņa redzams pat 40km attālais Zilais kalns.”
Skolēnus visvairāk pārsteidza tieši beidzamais teikums. Daži ticēja, citi apšaubīja iespējamību redzēt tik tālu, bet Pauls vēl pastāstīja, ka viņa tētis, stāvot uz šī baznīcas sliekšņa, esot redzējis pat Rīgas Pētergaili.
Palīdziet izšķirt strīdu un matemātiski pamatojiet, cik reāla ir iespējamība redzēt tik tālu. Kā Jūs domājat, vai skolēni noteikti redzēs Zilo kalnu, uzkāpdami baznīcas zvanu tornī?
6.stunda. Teorēmas par riņķī ievilktu un ap riņķi apvilktu četrstūri.
10. uzdevums.
Veicot uzdevumu, skolēni:
- veidos aprakstam atbilstošus zīmējumus;
- pamatos apgalvojumus, lietojot matemātisko valodu un simbolus;
- atkārtos zināmās sakarības riņķī;
- uzzinās sakarības par hordas-pieskares leņķi, leņķi, ko veido divas hordas, divas sekantes ( divas pieskares);
- meklēs informāciju mācību literatūrā;
- veidos matemātiski korektus apgalvojumus.
Ieteikumi skolotājam.
- Var izvēlēties tikai dažus no piedāvātajiem apgalvojumiem, jo l) un m) piemēri ir skolēniem grūti saprotami un to rezultāts ir retāk lietojams.
- Uzdevumu var piedāvāt darbam grupās. Katra grupa pēta savus apgalvojumus un ar rezultātiem iepazīstina pārējos audzēkņus. Kopīgi veido un papildina formulu lapu.
Uzdevums.
Izveido katram piemēram atbilstošu zīmējumu un nosaki, kurš no apgalvojumiem ir patiess? Patiesos apgalvojumus pamato, bet aplamos pārveido tā, lai tie būtu patiesi! Pieraksti patiesos apgalvojumus savā formulu lapā! Ja nepieciešams, meklē informāciju mācību grāmatās!
a) Riņķa līnijas diametrs, kas perpendikulārs pret hordu, dala šo hordu uz pusēm.
b) Vienas un tās pašas riņķa līnijas divas vienādas hordas redzamas no centra vienādos leņķos.
c) Jebkura horda savelk vienu riņķa līnijas loku.
d) Visi ievilktie leņķi, kas balstās uz vienu un to pašu loku, ir vienādi.
e) Ja divi ievilkti leņķi balstās uz kopēju hordu, bet dažādiem lokiem, tad to lielumu summa ir 180°.
f) Ievilkts leņķis, kas balstās uz diametru, ir šaurs.
g) Ievilkta leņķa lielums ir vienāds ar tāda centra leņķa lielumu, kas balstās uz tā paša loka, uz kura balstās ievilktais leņķis.
h) Hordas pieskares leņķi veido no viena riņķa līnijas punkta novilkta horda un pieskare.
i) Katra horda un pieskare veido vienu vienīgu hordas-pieskares leņķi.
j) Hordas-pieskares leņķa ABC lielums vienāds ar tāda ievilkta leņķa lielumu, kas balstās uz tā paša loka, kuru ietver leņķis ABC.
k) Divas hordas krustojoties veido 4 dažādus leņķus.
l) Divu hordu veidotais leņķis BAE ir vienāds ar tādu loku leņķisko lielumu summas pusi, kurus ieslēdz atbilstošais krustleņķu pāris DAC un BAE (skat.zīm.).
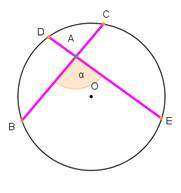
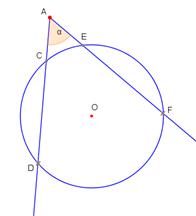
m) Leņķa DAF lielums, ko veido divas sekantes, ir vienāds ar
tādu loku ![]() un
un
![]() leņķisko
lielumu starpības pusi, kuri atrodas starp šī leņķa malām (skat.zīm.).
leņķisko
lielumu starpības pusi, kuri atrodas starp šī leņķa malām (skat.zīm.).
11.uzdevums.
Veicot uzdevumu, skolēni:
- saskatīs sakarības ievilktiem un apvilktiem daudzstūriem;
- formulēs hipotēzi;
- pierādīs teorēmas par ievilktiem un apvilktiem daudzstūriem.
Ieteikumi skolotājam.
- Puse no skolēniem meklē sakarību ievilktiem daudzstūriem, otra puse – apvilktiem.
- Aicināt skolēnus mainīt attēlus un mērīt vajadzīgos lielumus. To var darīt gan , izmantojot datora rīkus (ActivInspire programmatūra), gan parasto lineālu. Svarīgi, lai skolēni paši nonāk līdz hipotēzei.
- Pierādījumus veic skolēni kopā ar skolotāju.
Uzdevums.
Izmantojot Geonext failu T-8.5.gxt, noskaidrojiet, kāda sakarība ir spēkā visiem ievilktiem (apvilktiem) daudzstūriem.
7.stunda. Ievilktu un apvilktu daudzstūru elementu aprēķināšana.
12.uzdevums.
Veicot uzdevumu, skolēni:
- Attīstīs matemātisko valodu, lietos jēdzienus: apvilkts (ievilkts) trijstūris, četrstūris, sešstūris.
- Atkārtos zināmās formulas vai atradīs tās uzziņas literatūrā;
- Izteiks no formulas vajadzīgo lielumu.
- Izveidos pārskatu ar biežāk lietojamām formulām par ievilktiem un apvilktiem trijstūriem, četrstūriem, sešstūriem.
Ieteikumi skolotājam.
· Atkarībā no skolēnu spējām un atvēlētā laika, var aicināt papildināt tabulu ar sakarībām par ievilkta un apvilkta daudzstūra laukuma aprēķināšanu; var pierakstīt formulas, kas saista regulāra n-stūra malu ar ievilktas vai apvilktas riņķa līnijas rādiusu; var papildināt ar sakarībām, kā aprēķināt regulāra ievilkta un apvilkta daudzstūra leņķu lielumus.
· Stundas gaitā piedāvāt aprēķina uzdevumus, kuros lietot formulas regulāru apvilktu un ievilktu daudzstūru elementu aprēķināšanai.
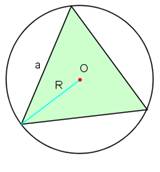
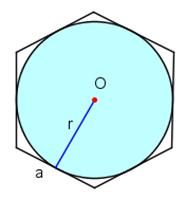
Uzdevums. Aizpildi iesākto tabulu!
Sakarības starp regulāra daudzstūra malu garumu un ievilktas vai apvilktas riņķa līnijas rādiusu.
a – regulārā daudzstūra malas garums;
R – ap daudzstūri apvilktas riņķa līnijas rādiuss;
r – daudzstūrī ievilktas riņķa līnijas rādiuss.
|
Daudzstūra malu skaits |
Skaidrojums ar vārdiem |
Shematisks zīmējums |
Rādiuss (zināms malas garums) |
Malas garums (zināms rādiuss) |
|
3 |
Trijstūris ievilkts riņķī |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
Četrstūris apvilkts ap riņķa līniju |
|
|
a = 2r |
|
|
6 |
|
|
|
|
|
|
|
|
|