Roberts Škapars. Izmaksas. Teorija. (e-grāmata)
5.1. Izmaksu funkcija
Iepriekšējās nodaļās jau ir apskatīts, kā mainās saražotās produkcijas kopējais apjoms, ja tiek palielināts ražošanas faktora, piemēram, darba ieguldījums. Šo likumsakarību var skaidrot arī no pretējā redzespunkta, t.i., cik daudz darba jāiegulda, lai izgatavotu noteiktu produkta apjomu. Lai ražotu kādu produkta apjomu, ražotājam ir jāiegādājas ražošanas faktori to tirgū par kādu cenu e. Iegādāto darba un citu ražošanas faktoru vērtības, kas nepieciešamas kāda produkta apjoma ražošanai, sauc par izmaksām. Ražotājs ražo produktu, sedzot mainīgās (variablās) VC un pastāvīgās (fiksētas) izmaksas FC. Mainīgās izmaksas ir vienlīdzīgas summai, kuru gūst, ja ražošanas faktoru daudzumu reizina ar tiem atbilstošām cenām.
(5.1.1) VC=e1v1+e2v2
Tātad mainīgās izmaksas ir atkarīgas no ražošanas faktoru kombinācijas (v1,v2) un to cenām (e1,e2). Tās palielinās vai samazinās līdz ar saražotā produkta kopējā apjoma pārmaiņām.
Pastāvīgās izmaksas nav atkarīgas no saražotā produkta kopējā apjoma pārmaiņām. Tās ir konstants lielums. Pastāvīgās izmaksas ir, piemēram, izmaksas par rūpnīcas uzturēšanu, tās apsardzi, apdrošināšanas maksājumi u.c. Kopējās izmaksas ir vienādas ar mainīgo un pastāvīgo izmaksu summu:
(5.1.2) TC=VC+FC.
Ja šīs izmaksas tiek racionāli izlietotas, tad rakstāma šāda funkcija:
(5.1.3) Q=f(VC,FC)=f(TC) vai
(5.1.4) TC=f--1(Q).
Kā redzams no vienādojuma (5.1.4), izmaksu funkcija ir inversa ražošanas funkcijai un tās grafiskais attēls ir ražošanas funkcijas spoguļattēls attiecībā pret taisni (simetrijas asi), kas novilkta 45 grādu leņķī pret koordinātu asīm. Ja pieņem, ka ir tikai viens mainīgs ražošanas faktors v1, tad ražošanas funkcija ir šāda:
(5.1.5) Q=f(e1,v1,FC).
To var parādīt grafiski, par piemēru izmantojot klasisko produktivitātes likuma grafisko attēlu, kurš koordinātu plaknē parādīts ar šai ražošanas funkcijai atbilstošo kopējo izmaksu funkcijas grafisko attēlu (5.1.1. attēls).
Uz y un x asīm 0a un 0b nogriežņi ir vienādi ar pastāvīgām izmaksām.
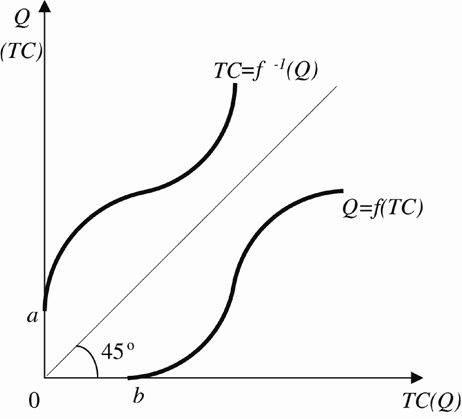
5.1.1. attēls. Saražotā produkta kopējā apjoma un izmaksu līknes