Riņķis un daudzstūris mākslā, dabaszinātnēs un matemātikā. Skolotāja atbalsta materiāls.
3.stunda. Četrstūru konstruēšana pēc dotajiem elementiem.
4.uzdevums.
Veicot uzdevumu, skolēni:
- mācīsies plānot uzdevuma risinājuma gaitu;
- atkārtos par leņķiem un to īpašībām;
- izmantos trijstūru līdzību uzdevumos par četrstūriem;
- uzziņas literatūrā noskaidros Talesa teorēmas būtību;
- attīstīs matemātisko valodu.
Ieteikumi skolotājam.
- Risinājumu piedāvā uz atsevišķām kartiņām, lai skolēni tās secīgi sakārto.
- Kopīgi ar skolēniem jāpārrunā katrs risinājuma solis, aicinot viņus izstāstīt risinājumu.
- Var piedāvāt skolēniem pēc apraksta veidot zīmējumu pašiem.
Uzdevums.
3.kursa audzēknis Kārlis devās uz matemātikas stundu, kurai bija sagatavojis uzdevuma par trapeci atrisinājumu. Uzdevums bija grūts un atrisinājums garš, tāpēc Kārlis to bija sarakstījis pa soļiem uz mazām lapiņām, aizmirsdams tās sanumurēt pēc kārtas. Kārlis bija lepns par paveikto līdz brīdim, kad klasē sacēlās caurvējš un visas risinājuma lapiņas aizpūta pa klasi. Palīdzēsim Kārlim sakārtot risinājumu!
Kārļa risinātais uzdevums.
Dota trapece, kuras malas AB║CD un malas AB garums ir 3 reizes lielāks nekā malai CD (skat.zīm.). Malas AB viduspunkts F ir savienots ar trapeces virsotnēm C un D. Malas CD viduspunkts E ir savienots ar trapeces virsotnēm A un B. Nogriežņi AE un DF krustojas punktā M, nogriežņi BE un FC krustojas punktā N. Aprēķināt nogriežņa MN garumu, ja malas AB garums ir a.
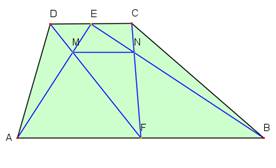
Lapiņas sagriešanai.
Risinājuma plāna punkti uz lapiņām. Sakārtojiet lapiņas (sanumurējiet) pareizajā secībā!
AB = a, tad AF = FB = DC = Aplūkosim ∆FNB un ∆CNE. FB║CE, FC un BE krustojas, tātad Līdz ar to ∆FNB~∆CNE
![]()
![]() , tad DE = EC =
, tad DE = EC = ![]()
![]() BFC =
BFC = ![]() FCE un
FCE un ![]() FBE =
FBE = ![]() BEC (iekšējie
šķērsleņķi).
BEC (iekšējie
šķērsleņķi).
Aplūkosim ∆AEB. AB║MN, tāpēc ∆AEB~ ∆MEN un Tā kā Savukārt, Ievietojot zināmos lielumus, iegūst ∆AMF~ ∆EMD, tātad ∆FNB~∆CNE, tātad
![]() .
.![]() , tad
, tad ![]() .
.![]()
![]() jeb
jeb ![]()
![]()
![]()
Aplūkosim No iepriekšējām sakarībām seko, ka Tad pēc Talesa teorēmas: AB║MN. Aplūkosim ∆AMF un ∆EMD. AF║DE, AE un FD krustojas, tātad Līdz ar to ∆AMF~∆EMD
![]() AEB.
AEB.![]()
![]() EAF =
EAF = ![]() AED un
AED un ![]() AFD =
AFD = ![]() FDE (iekšējie
šķērsleņķi).
FDE (iekšējie
šķērsleņķi).
5.uzdevums.
Veicot uzdevumu, skolēni:
- Konstruē rombu, ja dota diagonāle un augstums.
Ieteikumi skolotājam.
- Stundas gaitā var piedāvāt vēl citus uzdevumus konstruēt daudzstūrus.
- Dažos uzdevumos var skolēniem lūgt izveidot tikai konstrukcijas plānu.
- Var piedāvāt skolēniem izveidot arī dekora skici, ievērojot atbilstošus sienas izmērus un mērogu.
Uzdevums.
Celtniecības koledžas audzēkņi gribēja savai skolai atstāt dāvanu – pašu zīmētu sienas dekoru. Lai tas piestāvētu pārējai telpai, viņi nolēma, ka dekors jāveido romba formā. Skolēni izmērīja šī romba augstumu un diagonāli. Kā viņiem uzkonstruēt pašu rombu?