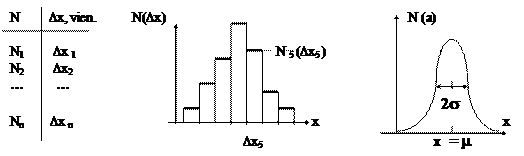16.nodaļa STOHASTISKAS SVĀRSTĪBU KUSTĪBAS
(gadījumrakstura jeb nenoteiktas ķermeņu kustības)
16.1.att. Gadījumrakstura jeb stohastiskā taisnlīnijas svārstību kustība
Vispārīgā skatījumā stohastiska rakstura var būt arī virzes kustība un virzes - svārstību kustību veidotā komplicēta kustība.
No vienkāršo kustību sapratnes un izpratnes mēs nonākam pie arvien sarežģītāku kustību apzināšanas.
Šī ir cilvēka sistēmiskās domāšanas īstenojuma būtība un sūtība.
16.1. STOHASTISKO KUSTĪBU MATEMĀTISKĀ MODELĒŠANA
(vienkāršāko stohastisko - gadījumrakstura jeb varbūtejisko procesu matemātiskie aprakstu – modeļu veidošana)
Stohastisko parādību iepazīšana ir īpaši svarīga, jo ļoti daudzi cilvēku dzīvē nozīmīgi procesi ir stohastiska rakstura procesi, taču to izpratnei skolās vēl joprojām tiek veltīta nepietiekama uzmanība.
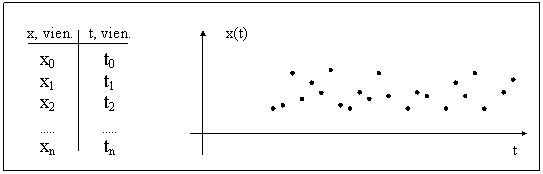
Ja veicam stohastiska procesa raksturlieluma x daudzus atkārtotus mērījumus laikā t un tādējādi iegūto mērskaitļu kopu x(t) atveidojam grafiski, tad iegūstam šķietami nesakarīgu punktu kopumu. Šajā gadījumā vairāki blakusesošie punkti neveido gludu līniju, bet visi punkti kopumā rada ļoti izplūdušu ainu (16.1.1.att. - horizontāli izstieptu punktu “mākoni”).
16.1.1.att.
Kopumā ir (n+1) laika momenti, kuros nosaka atbilstošās raksturlieluma a vērtības. Uzmanīgi ieskatoties, redzam, ka daudzos laika momentos raksturlieluma x vērtības haotiski atkārtojas un arī to, ka nav stingras noteiktības, kāda būs šī raksturlieluma x vērtība nākamajā laikā stāvoklī jeb momentā. Šādu parādības raksturlieluma mainību laikā x(t) tad arī sauc par stohastisku jeb gadījumrakstura procesu un runā par raksturlieluma stohastiskām svārstībām.
Stohastisku jeb gadījumrakstura procesu matemātiskie modeļi arī ir atbilstošas matemātiskās funkcijas. Tās sauc par stohastiskā procesa raksturlieluma x vērtību statistiskā sadalījuma funkcijām, kuras nosaka, attiecīgi apstrādājot iegūto mērskaitļu kopu x(t).
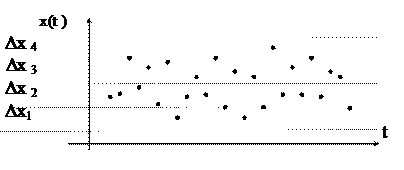
Stohastiskos procesus raksturojošās statistiskā sadalījuma funkcijas jeb, īsāk sakot, statistiskos sadalījumus, praksē noskaidro, vispirms veidojot novērojumu datiem x(t) atbilstošās histogrammas - stabiņveida statistiskos sadalījumus. Statistiskos sadalījumus kā histogrammas veido, vispirms saskaitot cik reizes vienas un tās pašas vērtības mērskaitļi ir sastopami atbilstošās mērskaitļu kopas noteiktos mērskaitļu intervalos Da. Īpaši jāievēro, ka mērījumu skaitam jābūt pietiekami lielam, lai atkārtoti iegūtu visas īstenojošās mērskaitļu vērtības.
16.1.2.att.
Apzīmējot noteiktas vērtības atkārtojošos mērskaitļu skaitu attiecīgo mērskaitļu intervalā ar N , tiek iegūts atbilstošā stohastiskā procesa raksturojums - histogramma tabulas veidā. Pēc tam šo statistisko sadalījumu - histogrammu N (Dx) attēlo grafiski, kas nodrošina tās uzskatāmību un ērtu lietošanu tālākajā parādības apzināšanā.


16.1.3.att.
Ļoti svarīgi ir saprast, ka jēga ir tikai histogrammas stabiņu augšējām horizontālajām svītriņām, kamēr vertikālajām līnijām histogrammās būtībā nav jēgas (tās lieto tikai grafika labākai uzskatāmībai).
Jo ilgāk un precīzāk veikti raksturlieluma x mērījumi, jo vairāk iegūto mērskaitļu un jo mazākus var izvēlēties attiecīgos mērskaitļu intervalus Dx. Citiem vārdiem, intervaliem Dx samazinoties, tiem grafikā atbilstošās svītriņas N (Dx) savelkas punktos, kas savukārt veido noteiktu līniju. Šī līnija tad arī ir atbilstošā raksturlieluma sadalījuma funkcijas N (x) grafiskais atveids.
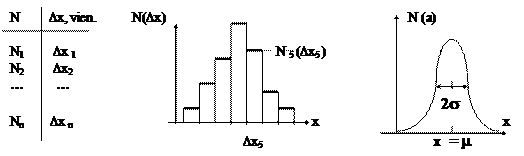
16.1.4.att.
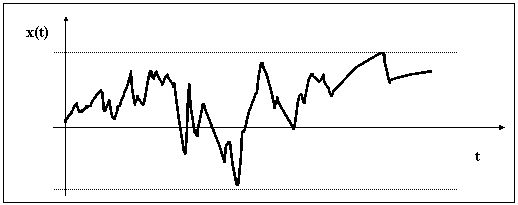
Stohastiskie procesi var tikt uzlūkoti arī kā stohastiskas svārstības - mainības stāvokļu gadījumrakstura svārstības ap kādu vidējo stāvokli.
Apzinot stohastiskos procesus mehānikā (iepazīstot punktveida ķermeņu gadījumrakstura kustību analīzi un sintēzi), mēs varam izdarīt ļoti nozīmīgu vispārinājumu - pārnest iegūtās atziņas arī vēl uz citu pasaules parādību zinātnisko apzināšanu!
Fizika ir fundamentāla zinātne ne tikai dabas un tehnikas jomā.


![]()