8.nodaļa PUNKTVEIDA ĶERMEŅU MEHĀNIKA
Punktveida ķermeņu savstarpējā novietojuma un tā mainības principiālais apraksts
Punktveida ķermeņa jēdziens.
Par punktveida ķermeni var uzskatīt ikvienu ķermeni, kura izmēri ir daudz mazāki par attālumiem līdz tam šī ķermeņa apkārtnē esošiem un dotajā situācijā vērā ņemamiem citiem ķermeņiem. Punktveida ķermenis raksturojas ar noteiktu to veidojošo iekšējo vidi, bet tās aizņemtais tilpums un ārējā forma netiek ievēroti.
Īpašs gadījums ir viendabīgas iekšējās vides veidoti lodveida ķermeņi, kas ir uzskatāmi par punktveida ķermeņiem arī tuvumā, līdz pat šo ķermeņu saskarei.
Attāluma un virziena jēdzieni.
Punktveida ķermeņu savstarpējais novietojums raksturojas ar šo ķermeņu savstarpējiem attālumiem un virzieniem, kuros ap katru no tiem atrodas pārējie ķermeņi. Par ķermeņu savstarpējo novietojumu (attālumiem un virzieniem) ir jēga runāt, ja ir vismaz divi aplūkojamie ķermeņi.
Šajā sakarā lai atceramies ģeometrijas pirmsākumus pamatskolas matemātikā. Ar to tad arī jau sākas mehānikas parādību matemātiskais apraksts jeb matemātiskā modelēšana!
Atskaites sistēmas jēdziens.
Ķermeņu savstarpējā novietojuma apraksta izveide sākas ar atskaites ķermeņa izvēli, kam seko koordinātu sistēmas piesaiste izvēlētajam atskaites ķermenim. Viena no visplašāk lietotajām ir Dekarta jeb taisnleņķa koordinātu sistēma, ko veido trīs (divas) savstarpēji perpendikulāras mērskaitļu asis. Izvēlētais atskaites ķermenis un ar to saistītā koordinātu sistēma kopumā veido ķermeņu savstarpējā novietojuma aprakstam nepieciešamo atskaites sistēmu. Lai labāk izprastu atskaites sistēmas būtību un sūtību, iejūtieties pats kā atskaites ķermenis! Atcerēsimies: saprātīgais cilvēks pasauli vispirms izjūt , pēc tam - izprot.
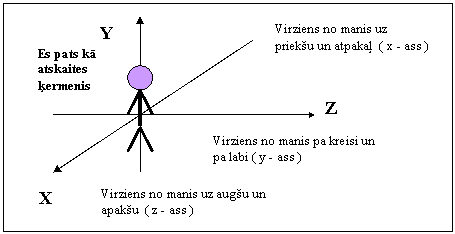
8.1.att.
Ķermeņu telpiskā stāvokļa raksturlielums ir rādiusvektors (R vai r).
Ķermeņu savstarpējo novietojumu izvēlētajā atskaites sistēmā raksturo jeb apraksta ar katra ķermeņa attālumu līdz atskaites ķermenim un virzienu attiecībā pret koordinātu asu pozitīvajiem virzieniem Šajā sakarā savukārt lai atceramies fizikas ābeces pamatatziņu: cilvēks apzina pasauli pa daļām, tās savstarpēji salīdzinot un kopsaistot. Saka, ka ķermeņi atrodas noteiktos telpiskajos stāvokļos, kurus raksturo atbilstošie radiusvektori - noteikta garuma, virziena un vērsuma taisnes nogriežņi. Ikviens rādiusvektors sākas no atskaites ķermeņa un beidzas ķermenī, kura telpisko stāvokli šis radiusvektors raksturo (uzdod, apraksta).
Ķermeņu rādiusvektori kā ķermeņu telpiskā stāvokļa raksturlielumi ir šo ķermeņu savstarpējā novietojuma apraksta pamatelementi. Konkrētais apraksts ir spēkā izvēlētajā atskaites sistēmā, citās atskaites sistēmās (izvēloties citus atskaites ķermeņus) attiecīgā apraksta raksturlielumu vērtības būs atšķirīgas.
Ķermeņu telpisko stāvokļu kopums uzdod vienu no fizikālajām telpām - parasto mehānikas telpu. Saka, ka ķermeņi atrodas trīsdimensionālā telpā. Vienkāršākā gadījumā runā par divdimensionālu telpu jeb ķermeņu atrašanos plaknē. Visvienkāršākajā gadījumā ir viendimensionāla telpa, kad ķermeņi atrodas uz līnijas. Kāda telpa jāizvēlas ķermeņu savstarpējā novietojuma aprakstam, to nosaka šie ķermeņi un cilvēku ērtības un vienkāršības apsvērumi, izvēloties atbilstošu atskaites sistēmu.
Ķermeņi, to savstarpējais novietojums ir konkrēti - novērojami, kamēr telpa kā ķermeņu iespējamo atrašanās vietu kopums ir abstrakcija novērotā atveidei cilvēka apziņā.
Zinot ķermeņu stāvokļus attiecībā pret izvēlēto atskaites ķermeni, ir iespējams raksturot arī visu ķermeņu savstarpējo novietojumu – ķermeņu attālumus un virzienus ikvienam ķermenim attiecībā pret jebkuru citu ķermeni.
Ikviena ķermeņa telpiskais stāvoklis ir zināms, ja zināmi trīs šī ķermeņa stavokļa raksturlielumi: rādiusvektora projekcijas rX, rY, rZ vai rādiusvektora modulis r.
VEKTORIKA - ķermeņu telpisko stāvokļu matemātiskā apraksta valoda.
Matemātikas nozari, kura aplūko vektorus kā matemātiskos lielumus, sauc par vektoru algebru.
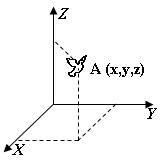
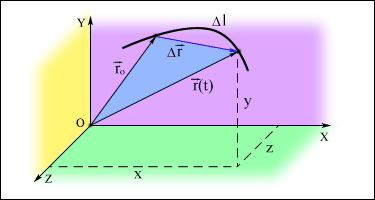
8.2.att. Masasa punkta stāvoklis 3D telpā un ķermeņa telpiskā stāvokļa rādiusvektors


