Roberts Škapars. Pilnīga konkurence, monopols, monopolstiskā konkurence un oligopols. Teorija. (e-grāmata)

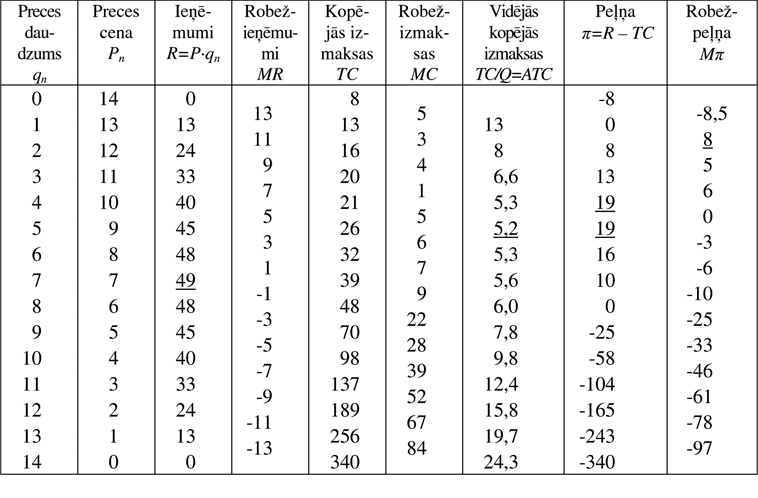
Tālāk noteiksim peļņas maksimumu piedāvājuma monopolā grafiski (6.4.1. attēls), izmantojot 6.4.1. tabulas datus.

6.4.1. attēlā a ir attēloti ieņēmumu R un izmaksu TC grafiki. Redzams, ka, pārdodot produkcijas 1 un 8 vienības, peļņa ir vienlīdzīga ar nulli, jo R=TC. Tie ir preces pārdošanas kritiskie apjomi monopolā. Maksimālā peļņa tiek sasniegta, kad attālums starp ieņēmumu R un izmaksu TC grafikiem ir vislielākais.

6.4.1. Maksimālās peļņas noteikšana piedāvājuma monopolā

Mūsu piemērā tas ir sasniegts, pārdodot 5 preces vienības. Tādējādi starp kritiskajiem pārdošanas apjomiem 1 un 8 veidojas peļņas lauks (6.4.1. attēls a, b). Tā lielums un pastāvēšanas iespēja ir atkarīga no līkņu R un TC formas un to izvietojuma koordinātu plaknē.

 

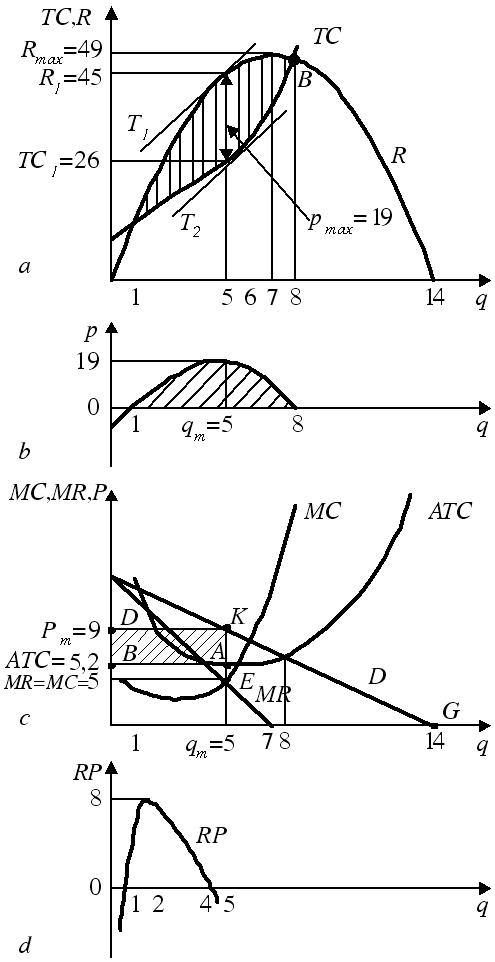
6.4.1. attēls. Peļņas maksimizācija piedāvājuma monopolā:

a – ieņēmumi un kopējās izmaksas; b – peļņa; c – robežizmaksas,

robežieņēmumi, vidējās izmaksas; d – robežpeļņa

Maksimālās peļņas sasniegšanas nosacījumus var iegūt, izmantojot arī robežieņē­mumus MR un robežizmaksas MC. Maksimālā peļņa tiek sasniegta, ja robežpeļņa Mπ ir vienlīdzīga ar nulli.

(6.4.2) 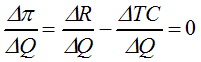            jeb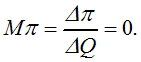      

No (6.4.2) izriet, ka

(6.4.3)       MR = MC.

Tādējādi peļņas maksimizāciju monopolā var definēt šādi: monopolists gūst maksimālo peļņu, ja tas pārdod tādu preces daudzumu, kura robežizmaksas MC un robežieņēmumi MR no tā pārdošanas ir vienādi.

Šo lielumu grafiki, izmantojot 6.4.1. tabulas datus, ir parādīti 6.4.1. attēlā c. Redzams, ka monopolā atšķirībā no pilnīgas konkurences cena ir lielāka par robežieņēmumiem. Diagrammā redzams, ka robežizmaksu MC un robežieņēmumu MR taišņu krustpunkta E projekcija uz pieprasījuma taisnes D (punkts K) rāda cenu, kas nodrošina maksimālo peļņu (P_m=9) un atbilstošo pieprasītās preces daudzumu (q_m=5). To sauc par Kurno punktu, jo franču ekonomists Augusts Kurno (1801 – 1877) pirmais skaidroja šo cenas veidošanās procesu monopola gadījumā.

Kopējo peļņu nosaka, reizinot vienas preces vienības pārdevuma peļņu ar realizētās preces daudzumu: . Peļņu, ko var iegūt no vienas pārdotās preces vienības π_v, aprēķina kā vidējo ieņēmumu AR un vidējo izmaksu ATC starpību: π_v=AR-ATC. Tā kā AR=P, tad π_v=P-ATC.

Peļņas lielumu var attēlot grafiski, izmantojot vidējo peļņu π_v (6.4.1. attēls c). Mūsu gadījumā vidējā peļņa vienlīdzīga ar nogriežņa AK skaitlisko vērtību, un kopējā peļņa ir:

No minētajām likumsakarībām izriet vēl šādi svarīgi secinājumi:

1. robežizmaksu un robežieņēmumu taišņu krustošanās ir iespējama tikai to pozitīvo skaitlisko nozīmju gadījumā, jo robežizmaksas nevar būt negatīvas, bet robežieņēmumi savukārt saglabā pozitīvu nozīmi tik ilgi, kamēr ieņēmumi, samazinoties cenai, vēl turpina pieaugt. Tas ir iespējams tikai pieprasījuma taisnes elastīgajā apgabalā, kad e_pc>1;

2. no iepriekš apskatītajiem maksimālās peļņas nosacījumiem izriet, ja 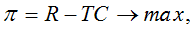  tad Mπ=MR-MC=0;

(6.4.4)          MR = MC.