Pārsteidzošās figūras - trijstūri un leņķi. Skolotāja atbalsta materiāls: 7.-8.stunda. Trijstūris – palīgs mērījumos.

7.-8.stunda. Trijstūris – palīgs mērījumos.

10.uzdevums.

Veicot uzdevumu, skolēni:

1) saista matemātikas zināšanas un prasmes par sakarībām trijstūros ar praktiskiem mērījumiem dabā;

2) plāno savu darbību praktiskas problēmas atrisināšanai;

3) sadarbojas, veicot praktisko darbu dabā;

4) prezentē darba rezultātus;

5) novērtē un izdara secinājumus par praktiskajā darbā iegūtajiem rezultātiem;

6) lieto dažādas garuma mērvienības un noskaidro attiecības starp tām.

Skat. Darba lapu skolēnam „Pārsteidzošais trīsstūris – palīgs mērījumos”.

Ieteikumi skolotājam:

· Izvēlieties reālus skolas apkārtnē esošus objektus.

· Daliet skolēnus grupās tā, lai būtu izmērīts gan augstums, gan attālums.

· Varat skolēniem pašiem ļaut padomāt, kā izgatavot palīgierīci mērīšanai, izmantojot dotos resursus (tādā gadījumā darba lapā nerakstiet mērītāja izgatavošanas aprakstu).

· Piedāvājiet mērītājus izgatavot skolēniem pašiem, parādot, ka tas ir vienkārši un iespējams izmantot vienkāršus līdzekļus (dēlīša vietā var būt jebkura cita taisna virsma), kā ar4ī to, ka nedaudz atjautības un matemātikas zināšanas var pielietot praktisku problēmu risināšanai.

· Svarīgi ir skolēniem likt izveidot matemātisko modeli un pamatot, kas un kāpēc viņiem būs jāmēra, kādas matemātiskās likumsakarības viņi izmantos.

· Dažādām skolēnu grupām var piedāvāt veikt mērījumus vai nu metros, vai pēdās, vai vēl izmantojot citas garuma mērvienības. Tādā gadījumā var turpināt sarunu par mērvienībām, kādas ir to attiecības, kādas mērvienības ir lietderīgāk izmantot un kāpēc.

· Stundas beigās pievērsiet vēlreiz skolēnu uzmanību tam, ka abus mērījumus veica, izmantojot vienāda veida trīsstūri. Varat aicināt skolēnus izteikt priekšlikumus, kā vēl varētu izmērīt dabā augstumu un attālumu, ja nav pieejami moderni mērītāji vai citas tehnoloģijas.

Mērītāja izgatavošana

Lai izgatavotu mērītāju, Jums dēlītī jāiedzen nagliņas tā, lai tās atrastos vienādsānu taisnleņķa trijstūra virsotnēs (skat.zīm.).

Ja Jūsu rīcībā nav uzstūra taisnā leņķa mērīšanai un cirkuļa vai lineāla vienādo malu atlikšanai, Jūs varat izmantot vienkāršu papīru. Pārlokiet papīru uz pusēm, tad vēlreiz, lai locījuma vieta sakristu, tad atlokot papīru vaļā, Jūs locījuma vietā iegūsiet taisno leņķi. To pašu papīru varat izmantot arī vienādo sānu malu atlikšanai.

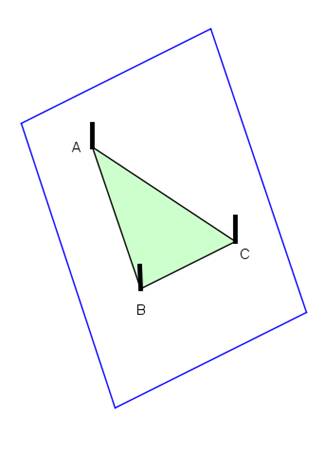
Zīm. Mērītājs

Var papildināt Mērītāju ar diegu un atsvaru augstuma mērīšanai, piestiprinot to punktā A. Tas dos iespēju veikt precīzāku mērījumu, novietojot mērītāja malu AB perpendikulāri zemei.

Darba lapa skolēnam

Pārsteidzošais trīsstūris – palīgs mērījumos

Pētniecisks darbs

1.grupa

Situācijas apraksts

Šodien jums ir īpašs uzdevums – noskaidrot pie skolas augošā koka augstumu, bet Jūsu rīcībā ir tikai dēlītis un 3 nagliņas.

Darba plānošana.

Uzrakstiet, kā Jūs rīkosieties, lai noteiktu koka augstumu, izmantojot pašu izgatavoto mērītāju.

Matemātiskais pamatojums.

Kā Jūs, izmantojot matemātiskas likumsakarības, pamatosiet sava mērījuma pareizību?

Un tagad dodieties veikt mērījumus!

Pierakstiet nepieciešamos mērījumus!

Koka augstums ir

Secinājumi par darbu un mērījuma precizitāti.

Darba lapa skolēnam

Pārsteidzošais trīsstūris – palīgs mērījumos

Pētniecisks darbs

2.grupa

Situācijas apraksts.

Šodien jums ir īpašs uzdevums – noskaidrot attālumu no skolas līdz kādam objektam (pēc skolotāja izvēles kāda konkrēta vieta vai objekts, kas atrodas tik tālu, ka tiešā veidā izmērīt attālumu ir pietiekami sarežģīti - attālums līdz ezera, upes otram krastam vai kāds attāls objekts), bet Jūsu rīcībā ir tikai dēlītis un 3 nagliņas.