Pārsteidzošās figūras - trijstūri un leņķi. Skolotāja atbalsta materiāls
4.stunda. Sinusu un kosinusa teorēmas.
4.uzdevums. (4.stunda)
Veicot uzdevumu, skolēni:
iegūst sinusu teorēmu, pierādot to.
Skat. Darba lapu skolēniem „Sinusu teorēma”
5.uzdevums (4.stunda).
Veicot uzdevumu, skolēni:
iegūst kosinusa teorēmu, pierādot to.
Skat. Darba lapu skolēniem „Kosinusa teorēma”.
(Mājās skolēniem var piedāvāt pierādīt kosinusa teorēmu abām pārējām malām, paskaidrojot, kā to var izdarīt.)
6.uzdevums (4.stunda).
Veicot uzdevumu, skolēni:
1) plāno risinājuma gaitu, izmantojot sinusu un kosinusa teorēmas;
2) iegūst sakarību trīsstūra leņķu aprēķināšanai, ja zināmas tā 3 malas;
3) iegūst prasmi noteikt trīsstūra veidu, izmantojot kosinusa teorēmu.
Ieteikumi skolotājam
- Skolēniem jāatkārto, pēc kādām pazīmēm trīsstūrus iedala un kādi veidi pastāv. Var izmantot PowerPoint prezentāciju „Trijstūru veidi”.
- Pēc plāna sastādīšanas skolēni iepazīstina pārējos ar savu plānu, izvēlas racionālāko/ efektīvāko paņēmienu.
- var piedāvāt katram skolēnu pārim citus malu garumus. Piedāvājot dažādus trijstūrus, ir iespēja pārliecināties, ka kosinusu teorēmu ir vienkārši un ērti izmantot trijstūra veida noteikšanai (veidojas pozitīvas, negatīvas un ar 0 vienādas kosinusu vērtības).
Vizuālais materiāls demonstrēšanai skolēniem
Uzraksti plānu, kā noteikt trijstūra veidu, ja zināmi tā malu garumi!
Nosaki dotā trijstūra veidu, ja zināmi tā trīs malu garumi!
a) 22cm, 13cm, 10cm;
b) 3cm, 7cm, 
cm;
c) 17cm, 7cm, 11cm;
d) 6cm, 
cm, 11cm;
e) 13cm, 14cm, 13cm;
f) 12cm, 14cm, 26cm;
g) 15cm, 17cm, 8cm.
Darba lapa skolēnam
Sinusu teorēma
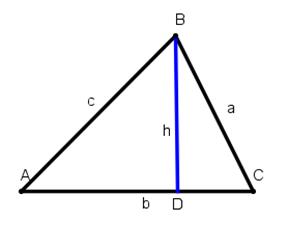
Dots trijstūris ABC, kura malu garumi ir a, b, c un leņķu lielumi ir A, B un C. (sk.zīm.)
1) Izsaki trijstūra ABC laukumu 3 dažādos veidos, izmantojot divas malas un leņķi starp tām!
S = ½ bc sinA
S = ... ... ... sin B
S = .....................
2) Salīdzini, kādas savstarpēji ir šīs izteiksmes!
Tātad
½ bc sinA ... ... ... sin B .....................
3) Izdali šajā vienādībā katru izteiksmi ar ½ !
4) Izdali šajā vienādībā katru izteiksmi ar reizinājumu abc (apdomā, vai tā drīkst dalīt un kāpēc) un daļas saīsini, cik iespējams!
...................
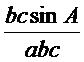
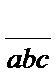Saīsinot:
5) Vienādība ir patiesa arī apgrieztajiem lielumiem, t.i.,
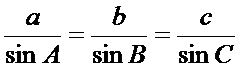
Esam ieguvuši sinusu teorēmu:
Jebkura trijstūra malas ir proporcionālas šo malu pretleņķu sinusiem.
Darba lapa skolēnam
Kosinusa teorēma
Dots trijstūris ABC, kura malu garumi ir a, b, c un leņķu lielumi ir A, B un C. BD ir trijstūra augstums h pret malu AC. (sk.zīm.)
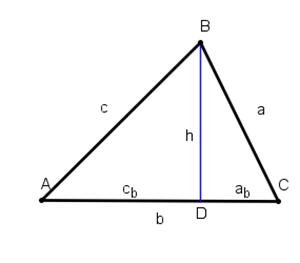
1) Novelkot augstumu BD, izveidojas divi trijstūri: ∆ABD un ∆DBC.
Kāda veida trijstūri tie ir?
2) ∆ABD pēc Pitagora teorēmas:
c2 =
3) ∆DBC pēc Pitagora teorēmas:
a2 =
4) No abām izteiksmēm izsaki h2:
No 2) izteiksmes
h2 = c2 – cb2
No 3) izteiksmes
h2 =
5) Kādas savstarpēji ir šīs izteiksmes?
Tātad iegūstam sakarību:
6) Uzmanīgi apskati trijstūra malu AC!
Ievēroji, ka
ab + cb = .....
Izsaki no šīs sakarības cb:
cb = ...............................
7) Aizstāj 5) punktā uzrakstītajā izteiksmē cb ar iegūto izteiksmi
8) Atver iekavas
9) Savelc līdzīgos locekļus
10) Izsaki c2:
11) Atlicis tikt galā ar lielumu ab. Izmantojot sakarības taisnleņķa ∆DBC, izsaki cos C!
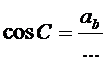
Tad ab = ....
12) Aizvietojot ab ar iegūto izteiksmi, nonākam pie sakarības:
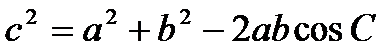
Esam ieguvuši kosinusa teorēmu:
Jebkura trijstūra malas kvadrāts vienāds ar divu pārējo malu kvadrātu summu, no kuras atņemts šo malu divkāršots reizinājums ar ietvertā leņķa kosinusu.