Stereometrijas pamati
4. Kopsavilkums
|
Stereometrijas
pamatjēdzieni, paralelitāte un perpendikularitāte telpā |
|||
|
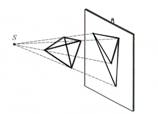
Centrālā projekcija |
Attēls, kuru iegūst, ja
visi projicējošie stari iziet no viena punkta. |
S ir punkts, no kura iziet
visi projekcijas stari, caur ķermeņa virsotnēm pret plakni. |
|
|
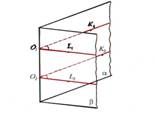
Divplakņu kakta leņķis |
|
Divplakņu kakta leņķi var
iegūt, novelkot plakni caur punktu O perpendikulāri divplakņu kakta šķautnei.
Zīmējumā: K1O1L1 un K2O2L2 |
|
|
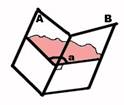
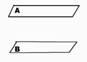
Divplakņu kakts |
Par divplakņu kaktu sauc
figūru, kuru veido divas pusplaknes ar kopīgu robežu, ja abas pusplaknes
neatrodas vienā plaknē. |
A un B ir pusplaknes,
kuras neatrodas vienā plaknē. |
|
|
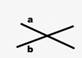
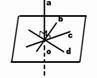
Krustiskas taisnes |
Divām taisnēm ir viens
kopīgs punkts. |
Taisnes a un b ir
krustiskas taisnes. |
|
|
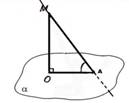
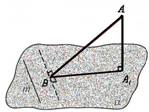
Leņķis starp taisni un
plakni |
Par leņķi starp taisni un
plakni sauc leņķi, starp taisni un tās projekciju plaknē. |
Taisnes MA projekcija ir
OA, leņķis starp taisni MA un OA ir OAM. |
|
|
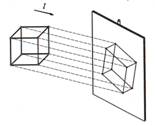
Paralēlā projekcija |
Attēls, kuru iegūst, ja
visu projicējošo staru virziens ir paralēls kādai taisnei. |
Taisne l ir projekcijas
virziena taisne, visi projekcijas stari ir paralēli tai. Projekcijas stari
tiek vilkti no ķermeņa virsotnēm pret plakni. |
|
|
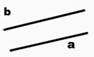
Paralēlas taisnes |
Divas taisnes sauc par
paralēlām, ja tās atrodas vienā plaknē un nekrustojas. |
Taisnes a un b ir
paralēlas taisnes. |
|
|
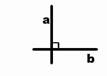
Perpendikulāras taisnes |
Divas taisnes sauc par
savstarpēji perpendikulārām, ja leņķis starp tām ir 90 grādi. |
Taisnes a un b ir
perpendikulāras taisnes. |
|
|
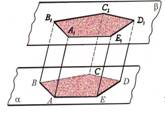
Plakņu paralelitāte |
Plaknes sauc par
paralēlām, ja tās nešķeļas. |
Plaknes A un B ir
paralēlas. |
|
|
Plakņu perpendikularitāte |
Divas plaknes sauc par
perpendikulārām, ja leņķis starp tām ir 90 grādu. |
Plaknes A un B ir
perpendikulāras. |
|
|
Projekcija |
Telpisku figūru attēlošana
plaknē. |
Ir divi projekciju veidi:
paralēlā projekcija un centrālā projekcija. |
|
|
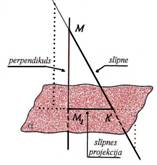
Slīpnes projekcija |
|
Punktus M1 un K sauc atbilstoši par perpendikula un slīpnes pamatu plaknē, bet
nogriezni M1K - par slīpnes projekciju plaknē. |
|
|
Šķērsas taisnes |
Divas taisnes sauc par
šķērsām taisnēm, ja tās neatrodas vienā plaknē. |
Taisnes a un b neatrodas
vienā plaknē, tās ir šķērsas taisnes. |
|
|
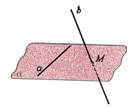
Taisnes un plaknes
paralelitāte |
Taisni un plakni sauc par
paralēlām, ja tās nekrustojas. |
Taisne b ir paralēla
plaknei a |
|
|
Taisnes un plaknes
perpendikularitāte |
Taisni sauc par
perpendikulāru plaknei, ja tā ir perpendikulāra katrai šīs plaknes taisnei. |
Ja taisne ir
perpendikulāra divām krustiskām taisnēm plaknē, tas tā ir perpendikulāra
plaknei. |
|
|
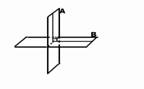
Triju perpendikulu
teorēma |
Ja taisne, kas atrodas
plaknē, ir perpendikulāra pret slīpnes projekciju, tad tā ir perpendikulāra
arī pret pašu slīpni. |
Taisne m ir perpendikulāra
pret taisni BA1, tā ir arī perpendikulāra pret slīpni. |
|
|
Prizma |
|||
|
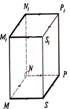
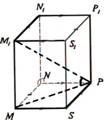
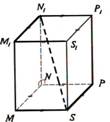
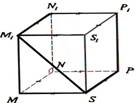
Četrstūra prizma |
|
Prizma, kuras pamats ir
četrstūris. Zīmējumā: MNSP un M1N1P1S1 |
|
|
Daudzskaldnis |
Par daudzskaldni sauc
telpisku ķermeni, kura virsma sastāv no plaknes daudzstūriem. |
|
|
|
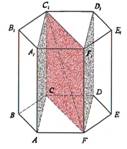
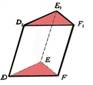
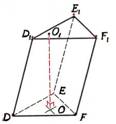
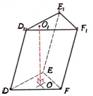
Diagonālšķēlums |
Prizmas šķēlumu ar plakni,
kas iet caur prizmas diagonāli un sānu šķautni, sauc par diagonālšķēlumu. |
AA1C1C, CC1F1F un FF1D1D |
|
|
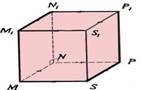
Leņķis starp prizmas
diagonāli un pamatu |
|
Leņķis starp prizmas
diagonāli un pamatu: <M1PM |
|
|
Pamata laukums |
|
Tiek aprēķināts pamata
daudzstūrim, pēc dotā daudzstūra laukuma aprēķināšanas formulām. |
|
|
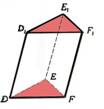
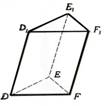
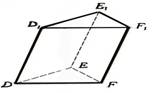
Pamata šķautne |
|
Pamatu šķautnes: DE,
EF,FD, D1E1, E1F1, F1D1 |
|
|
Pilnas virsmas laukums |
Par prizmas pilnas virsmas
laukumu S sauc prizmas visu skaldņu laukumu summu. |
Spilna=Ssānu+2Spam Ssānu - Sānu
virsmas
laukums Spam - pamata
daudzstūra laukums. |
|
|
Prizma |
Par n-stūra prizmu sauc
daudzskaldni, kura divas skaldnes ir vienādi n-stūri, kas atrodas paralēlās
plaknēs, bet pārējās n skaldnes ir paralelogrami. |
|
|
|
Prizmas augstums |
Perpendikulu, kas novilkts
no viena pamata kaut kāda punkta pret otra pamata plakni, sauc par prizmas
augstumu. |
Augstums: OO1 |
|
|
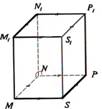
Prizmas diagonāle |
Nogriezni, kas savieno
divas daudzskaldņa virsotnes, kuras nepieder vienai skaldnei, sauc par
daudzskaldņa diagonāli. |
Diagonāle: N1S |
|
|
Prizmas pamats |
|
Daudzstūri, kuri atrodas
prizmas paralēlajās plaknēs. |
|
|
Regulāra prizma |
Taisnu prizmu, kuras
pamati ir regulāri daudzstūri, sauc par regulāru prizmu. |
|
|
|
Sānu skaldne |
|
Prizmas paralelogrami. |
|
|
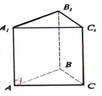
Sānu šķautne |
|
Sānu šķautnes: AA1, CC1, BB1 |
|
|
Sānu virsmas laukums |
|
Visu sanu skaldņu laukumu
summa. Sānu skaldņu izklājums veido taisnstūri(taisnai prizmai).
Aprēķina: Ssānu=Ppam*H |
|
|
Skaldnes diagonāle |
|
Nogrieznis, kas savieno
sānu skaldnes divas virsotnes, kuras nepieder vienai malai. |
|
|
Slīpa prizma |
|
Prizma, kuras sānu
šķautnes nav perpendikulāras pamatiem sauc par slīpu prizmu. |
|
|
Šķautne |
|
Prizmas daudzstūru kopīgas
malas sauc par šķautnēm. |
|
|
Taisna prizma |
|
Prizmu, kuras sānu
šķautnes ir perpendikulāras pamatiem, sauc par taisnu prizmu. |
|
|
Prizmas tilpums |
|
Prizmas tilpums ir vienāds
ar pamata laukuma un augstuma reizinājumu.
V=Spam*H |
|
|
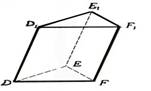
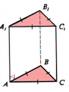
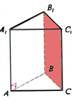
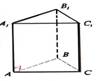
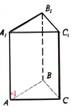
Trijstūra prizma |
|
Prizma, kuras pamata
daudzstūris ir trijstūris. |
|