Stereometrijas pamati
| Site: | Profesionālajā izglītībā iesaistīto vispārizglītojošo mācību priekšmetu pedagogu kompetences paaugstināšana |
| Course: | MateT006 : Skolēnam atvērts matemātikas mācību process profesionālajā izglītībā |
| Book: | Stereometrijas pamati |
| Printed by: | Guest user |
| Date: | Sunday, 8 March 2026, 8:34 AM |
Description
Teorētiskais materiāls stereometrijas pamatjēdzienu apguvei.
Titullapa



Stereometrijas pamati
Materiāls izstrādāts
ESF Darbības programmas 2007. - 2013.gadam „Cilvēkresursi un nodarbinātība”
prioritātes 1.2. „Izglītība un prasmes”
pasākuma 1.2.1.„Profesionālās izglītības un vispārējo prasmju attīstība”
aktivitātes 1.2.1.2. „Vispārējo zināšanu un prasmju uzlabošana”
apakšaktivitātes 1.2.1.1.2. „Profesionālajā izglītībā iesaistīto pedagogu
kompetences paaugstināšana”
Latvijas Universitātes realizētā projekta
„Profesionālajā izglītībā iesaistīto vispārizglītojošo mācību priekšmetu pedagogu
kompetences paaugstināšana”
(Vienošanās Nr.2009/0274/1DP/1.2.1.1.2/09/IPIA/VIAA/003,
LU reģistrācijas Nr.ESS2009/88) īstenošanai.
Rīga, 2010.
1. Ievada vietā. Tikai tas, kurš visu zina, var lidot droši
Pirms sapņa par brīvdienām tālās zemēs daudziem vispirms ir murgs par lidojumu. Kas tur tā klaudz! Kāpēc spārni tā plivinās? Kāpēc pilots pēkšņi piedod gāzi? Šeit īsa instrukcija visiem, kas gribētu zināt, kas notiek lidojuma laikā!
Leģendas dažreiz gan ir iesīkstējušas, arī tās par gaisa bedrēm. Gaisā nav bedru. Ja lidmašīna arī kādreiz krīt, tad tā lido cauri zonai, kurā gaiss krīt uz leju. Gaiss tā dara tāpēc, ka citās vietās tas ceļas uz augšu, piemēram, mākoņos un negaisā. Tajās vietās, protams, arī krata. Kas lido pirmoreiz vai retāk, dažas parādības nespēj izskaidrot. Šā iemesla dēļ ārzemēs tiek rīkoti pat semināri pret lidojumu bailēm, un vissvarīgākā lekcija šajos kursos ir informācija par to, kas notiek lidojuma laikā. Tikai tas, kurš visu zina, var lidot droši.
Nepazīstamās skaņas sākas jau tad, kad pasažieris grib ērtāk iekārtoties sēdeklī. Pēkšņi lidmašīnas ķermenī kaut kas draudīgi nodārd. Iemesls - pēc bagāžas iekraušanas tiek aizvērtas lielās lūkas zem salona. Nākamais solis ir dzinēja iedarbināšana. Tie, kas sēž tālu priekšā, var caur logu novērot, kā sāk griezties lielais turbīnas ventilators. Lai arī salons ir labi izolēts pret āra trokšņiem, var skaidri dzirdēt, kā turbīna uzņem apgriezienus. Skaņa pieaug līdz savdabīgai dziedāšanai. Ja iznāk sēdēt aiz spārna astes galā, tad pārsvarā var dzirdēt gāzu šņākšanu, kaukšanu, kas nāk ārā no dzinēja un rada vilkmi. Katrā ziņā ir patīkami apzināties, ka dzinēji strādā labi. Tiklīdz lidmašīna sāk kustēties, var dzirdēt ieslēdzamies elektromotoru. Tad jau var redzēt, kā tiek izbīdītas starta stāvoklī plāksnes, kas atrodas spārnu priekšpusē un aizmugurē. Tikai tā lidmašīna var radīt pietiekami lielu cēlējspēku, lai paceltos gaisā. Tad pilots no vadības saņem atļauju pacelties gaisā, piedod gāzi.
To nevar nepamanīt. Dzinēji attīsta pilnu jaudu, dažās lidmašīnās turbīna dārd diezgan iespaidīgi. Šīs skaņas spēj patikt tikai tiem, kam patīk sporta auto vai motociklu kaukšana. Daudziem pasažieriem šis turbīnas troksnis šķiet ļoti nepatīkams. Ir daudzas lidmašīnas, kuru starta trokšņi netraucē lidostas kaimiņos dzīvojošo cilvēku dzīvi, toties pasažierus gan. Ja, pieaugot ātrumam, lidmašīna arvien trakāk sāk kratīties, tad tam nav sakars ar riteņu kvalitāti, bet gan ar to, ka daži skrejceļi nav sevišķi labā stāvoklī. Plaisas un bedres padara startu līdzīgu braucienam pa lauku ceļu. Tikai tad, kad lidmašīna sasniedz 1. formulas ātrumu - 280 km stundā, cēlējspēks ir pietiekams, lai lidotu. Pilots ar vadības kloķi paceļ lidmašīnas degunu gaisā, lidmašīna paceļas, atraujas no zemes un sāk celties gaisā.
Zeme attālinās, un lidosta pārvēršas par rotaļu pilsētiņu. Atkal zem grīdas atskan skaļš troksnis, tiek ievilkti riteņi, aizveras lūkas. Jo ātrāk lidmašīna lido, jo mazāk nepieciešams papildus cēlējspēks. Tāpēc pilots pakāpeniski aizver papildu plāksnes uz spārniem, līdz tās pilnīgi sakļaujas. Uzmanīgs vērotājs var novērot stūres plāksnes, ar kurām lidmašīna tiek noturēta horizontāli, lai pagriezienos ierakstītu līknē. Tad šķērsstūris spārnu galos tiek sagriezts pretējos virzienos. Kreisajā pusē - uz leju, labajā - uz augšu. Tad ir jālido pa kreisi. Ja jālido pa labi, tad - otrādi. Stūrēm palīdz lielas plāksnes, kuras spārnu virsmā tiek iebīdītas uz augšu, tās sauc par spoileriem. Tiem gan maz kas kopīgs ar ātru automašīnu modes aksesuāriem. Lidmašīnu spoileri ir daudzfunkcionālas plāksnes, kas kalpo ne tikai stūrēšanai.
Tiklīdz lidmašīna sasniegusi lidojuma drošības dienesta norādīto augstumu, dzinēju trokšņi pieklust. Taču var gadīties, ka lidojuma laikā atkal tiek piedota gāze, proti, tad, kad pilots saņem rīkojumu pacelties augstāk. Jo augstāk lidmašīna lido, jo retāks ir gaiss, un ar gaisa pretestību samazinās arī degvielas patēriņš un dzinēju kaitīgā iedarbība.
Līdz šim viss noritēja normāli, bet var gadīties arī negaidīti notikumi. Gaisa virpuļi dažreiz spēcīgi satricina lidmašīnu, it sevišķi tad, kad tā lido cauri mākoņiem. Pilots parasti zina, ka būs gaidāmi šādi virpuļi, un par to paziņo pasažieriem. Tam parasti seko norādījums piesprādzēties, jo daži gaisa virpuļi var būt tik spēcīgi, ka var izkrist no sēdekļa un savainoties. Šādos virpuļos spārnu gali sāk bīstami locīties, bet par to, protams, konstruktori ir padomājuši. Pārbaudēs paredzēts, ka spārni bez bojājumiem var izliekties par vairākiem metriem, turklāt elastīgie spārni uztver arī virpuļu triecienus pret kabīni tāpat kā automašīnas amortizatori.
Ja dienā var novērot stūru un spoileru darbību, naktī paveras cits skats. Dažādas mīklainas gaismas, ritmiski sarkani zibšņi atspoguļojas uz spārniem un dzinējiem. Tie ir pretsadursmju gaismu atspīdumi, kas atrodas lidmašīnas augšpusē un apakšpusē. Un spārnu galos regulāri uzzibsnī baltas gaismiņas, kam ir tieši tāds pats uzdevums. Ar šīm gaismas zīmēm lidmašīnas ir redzamas vairāku kilometru attālumā.
Pie skaidrām debesīm var redzēt arī citas lidmašīnas, it sevišķi lielu lidostu tuvumā. Nolaišanās sākas tad, kad dzinēji pieklust. Lidmašīna pamet norādīto lidojuma augstumu, dažreiz tā tiek piebremzēta ar spoileriem. Tie samazina cēlējspēku, un lidmašīna nolaižas ātrāk. To var sajust arī tad, kad spoileru izraisīto virpuļu vibrācijas satricina kabīni.
Tuvojoties lidostai, daudz kas atkārtojas pretējā secībā. Tiek izbīdītas nolaišanās plāksnes un priekšspārni, lai, samazinoties ātrumam, noturētu lidmašīnu gaisā. Ar rībienu tiek izlaistas šasijas. Lidmašīna gatava nolaisties. Zem spārniem parādās betona skrejceļš. Pieskaroties zemei, vienlaikus notiek divas darbības. Pirmā - visi iespējamie spoileri tiek pacelti vertikāli gaisā, lai likvidētu cēlēspēku un palielinātu bremzēšanas pretestību. Otrā - dzinēju trokšņi spēji pastiprinās, jo pilots ieslēdzis pretvilkmi, tā laikā dzinēja gāzu strūkla tiek pagriezta uz priekšu tā, ka vilkme tagad darbojas kā bremze. Spoileri un reverss saīsina nolaišanās ceļu. Un tikai tad, kad ātrums ir pietiekami mazs, tiek nospiestas arī riteņu bremzes.
Spējo bremzēšanu var ne tikai sajust, bet arī sadzirdēt, jo bieži vien bremzes čīkst tāpat kā automašīnai.
Beidzot lidmašīna ir uz zemes! Reverss tiek izslēgts, spoileri un nolaišanās plāksnes tiek ievilktas, atliek tikai aizbraukt līdz stāvvietai.
2. Īsi par plakni un taisni, to savstarpējo novietojumu.
Ja punkts pieder taisnei vai plaknei, t. i., punkts atrodas uz taisnes vai atrodas plaknē, tad teiksim arī, ka caur punktu var novilkt taisni vai plakni jeb – taisne vai plakne iet caur šo punktu.
Ja taisne pieder plaknei, t. i., taisne atrodas plaknē, tad teiksim arī, ka caur taisni var novilkt plakni jeb – plakne iet caur šo taisni.
1. AKSIOMA
Caur jebkuriem diviem telpas punktiem var novilkt vienu vienīgu taisni.
2. AKSIOMA
Caur jebkuriem trim telpas punktiem, kas neatrodas uz vienas taisnes, var novilkt vienu vienīgu plakni.
3. AKSIOMA
Ja divi taisnes punkti pieder plaknei, tad visi šīs taisnes punkti pieder plaknei.
4. AKSIOMA
Ja divām plaknēm ir kopīgs punkts, tad tām ir kopīga taisne, uz kuras atrodas visi šo plakņu kopīgie punkti.
PLAKNES NOVILKŠANA
(caur taisni un punktu;
caur divām krustiskām taisnēm)
1. TEORĒMA
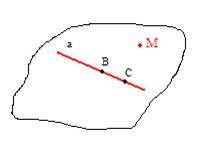
Caur taisni un punktu, kas tai nepieder, var novilkt vienu vienīgu plakni.
![]()
2. TEORĒMA
Caur divām krustiskām taisnēm var novilkt vienu vienīgu plakni.
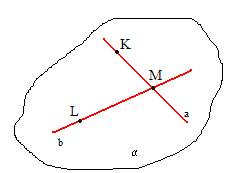
1. uzd.
Taisnes c un d krustojas punktā A, turklāt c atrodas plakne y.
Vai ir pareizs apgalvojums, ka a) taisne d atrodas plaknē y;
b) punkts A atrodas plaknē y?
2. uzd.
Pierādīt, ka caur taisni var novilkt bezgalīgi daudz plakņu.
TAIŠŅU PARALITĀTE
Definīcija
Divas taisnes sauc par paralēlēm, ja tās atrodas vienā plaknē un nekrustojas.
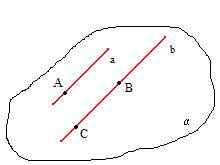
1. TEORĒMA
Caur divām paralēlām taisnēm var novilkt vienu vienīgu plakni.
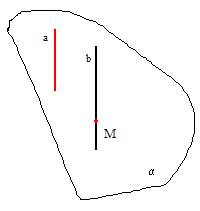
2. TEORĒMA
Telpā caur punktu ārpus taisnes var novilkt vienu vienīgu taisni, kas paralēla dotajai.
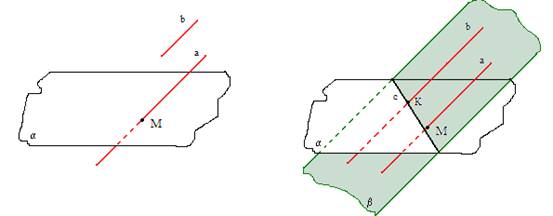
3. TEORĒMA
Ja viena no divām paralēlām taisnēm krusto plakni, tad arī otra taisne krusto šo plakni.
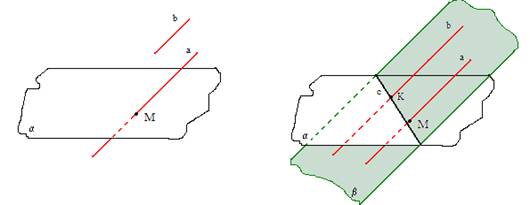
4. TEORĒMA
Ja katra no divām taisnēm ir paralēla trešajai taisnei, tad tās abas ir savstarpēji paralēlas.
1. uzd.
Taisne ir paralēla vienai regulāra astoņstūra malai. Cik astoņstūra diagonālēm šī taisne ir paralēla?
2. uzd.
Dotas trīs paralēlas taisnes. Cik plakņu var novilkt tā, lai tās saturētu vismaz divas no dotajām taisnēm?
TAISNES un PLAKNES PARALELITĀTE
Definīcija
Taisni un plakni sauc par paralēlām, ja tās nekrustojas.
1. TEORĒMA (taisnes un plaknes paralelitātes pazīme)
Ja taisne, kas neatrodas plaknē, ir paralēla kādai šīs plaknes taisnei, tad tā ir paralēla pašai plaknei.
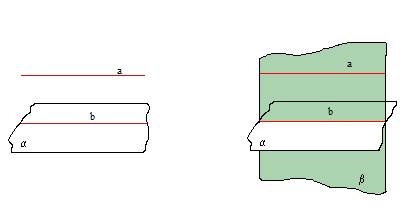
2. TEORĒMA
Ja plakne iet caur taisni, kas ir paralēla citai plaknei, un abas plaknes šķeļas, tad dotā taisne ir paralēla plakņu šķēluma taisnei.
1. uzd.
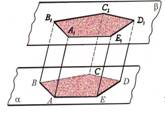
Rombs ABCD un taisnstūris CDEF atrodas dažādās plaknēs. Noteikt, kāda figūra ir četrstūris AEFB.
2. uzd.
Trapeces sānu malas viduspunktos krustojas ar plakni y. Pierādīt, ka trapeces pamati ir paralēli plaknei y.
PLAKŅU PARALITĀTE
Definīcija
Plaknes sauc par paralēlām, ja tās nešķeļas.
1.TEORĒMA
Ja kāda taisne krusto vienu no paralēlām plaknēm, tad tā krusto arī otru plakni.
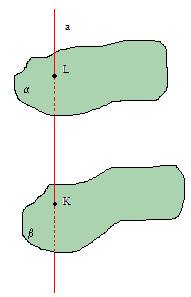
2. TEORĒMA
Ja kāda plakne šķeļ vienu no paralēlām plaknēm, tad tā šķeļ arī otru plakni.
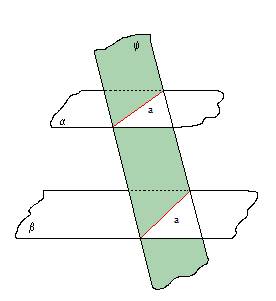
3. TEORĒMA (plakņu paralelitātes pazīme)
Ja vienas plaknes divas krustiskas taisnes ir attiecīgi paralēlas ar otras plaknes divām krustiskām taisnēm, tad šīs plaknes ir paralēlas.
4. TEORĒMA
Ja divas paralēlas plaknes šķeļ trešā plakne, tad plakņu šķēlumu taisnes ir paralēlas.
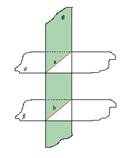
5. TEORĒMA
Paralēlu taišņu nogriežņi, kas atrodas starp paralēlām plaknēm, ir vienādi.
6. TEORĒMA
Caur punktu, kas neatrodas plaknē, var novilkt vienu vienīgu plakni, kas paralēla dotajai.
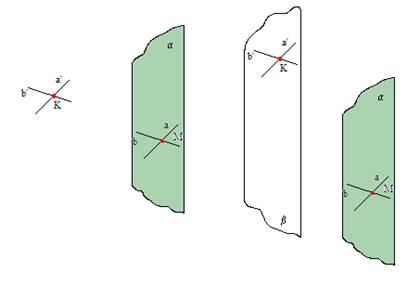
1. uzd.
Taisnes atrodas vienā no paralēlajām plaknēm. Pierādīt, ka taisne ir paralēla otrai plaknei.
2. uzd.
Trijstūra divas malas ir paralēlas plaknei y. Pierādīt, ka trijstūra trešā mala arī ir paralēla plaknei y.
ŠĶĒRSAS TAISNES
Definīcija
Divas taisnes sauc par šķērsām taisnēm, ja tās neatrodas vienā plaknē.
1. TEORĒMA (šķērsu taišņu pazīme)
Ja viena no divām taisnēm atrodas plaknē, bet otra taisne krusto šo plakni punktā, kas atrodas uz pirmās taisnes, tad dotās taisnes ir šķērsas.
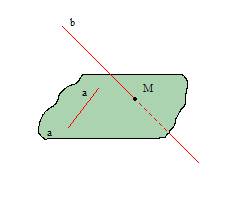
2. TEORĒMA
Caur katru no divām šķērsām taisnēm var novilkt vienu vienīgu plakni, kas ir paralēla otrai plaknei.
1. uzd.
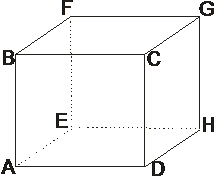
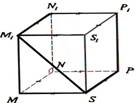
Dots kubs ABCDAA’B’C’D’. Noteikt šādu taišņu savstarpējo stāvokli:
a) AB un D’C’;
b) BC un DD’;
c) AA’ un A’D’;
d) AC un D’B’.
2. uzd.
Taisne m iet caur kvadrāta ABCD centru O. Noteikt taišņu m un AD savstarpējo stāvokli, ja
a) m neatrodas kvadranta plaknē;
b) m atrodas kvadranta plaknē un krusto malu BC;
c) m krusto kvadrāta malas AB un CD to viduspunktos.
Par teorēmu pareizību var pārliecināties arī praktiski, uztverot papīra lapu par plakni un locījuma līnijas par taisnēm.
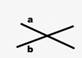
Divas taisnes
plaknē, kurām ir viens kopīgs punkts, sauc par krustiskām taisnēm.
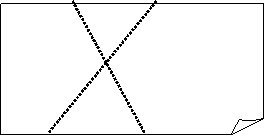
Krustisku taišņu locīšana:
1. Pārloka papīra lapu un
atloka to vaļā.
2. Veic vēl vienu locījumu
tā, lai jaunā locījuma līnija krustotos ar iepriekš uzlocīto. Papīra lapu
atloka vaļā. Var redzēt, ka ir uzlocītas divas krustiskas taisnes.
Šobrīd ierobežotā papīra lapa rada problēmu, jo ir iespējama tāda situācija, ka šīs taisnes ir krustiskas, bet tās krustojas ārpus lapas malām. Šeit ir jāpieņem, ka lapa ir neierobežota. Pārbaudīt, vai taisnes krustosies, var, pārbaudot, vai taisnes nav paralēlas. Ja taisnes nav paralēlas, tad tās ir krustiskas. Taišņu paralelitāti aplūkosim mazliet vēlāk.
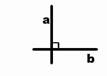
Krustiskas taisnes,
kuras krustojoties veido taisnu leņķi, sauc par perpendikulārām taisnēm.
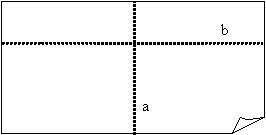
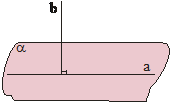
Perpendikulāru taišņu
locīšana:
1. Pārloka papīra lapu pa
vēlamo locījuma līniju a, pret kuru vēlas novilkt perpendikulāru taisni.
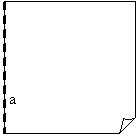
3. Pārloka locījuma līniju a “uz pusēm”. Ja perpendikulārā locījuma līnija jānoloka pret konkrētu punktu, tad pārloka locījuma līniju caur šo punktu.

3. Atlokot vaļā papīra lapu, var redzēt, ka ir nolocītas divas savstarpēji perpendikulāras locījuma līnijas a un b.
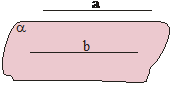
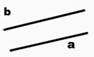
Divas dažādas
taisnes plaknē, kuras nekrustojas, sauc par paralēlām. Lai varētu uzlocīt divas paralēlas
taisnes, tiek izmantotas perpendikulāras taisnes.
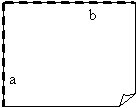
Paralēlu taišņu locīšana:
1. Sākumā locīšanu veic tādā
pašā veidā, kā lokot perpendikulāras taisnes. Konstruē divas perpendikulāras
locījuma līnijas a un b, bet papīra lapu neatloka vaļā (skat. perpendikulāru
taišņu locīšana 1., 2. punktu).
2. Pret locījuma līniju b noloka vēl vienu perpendikulāru locījuma līniju c, t.i., pārloka locījuma līniju.
3. Atlokot vaļā papīra lapu, var redzēt, ka ir uzlocītas divas savstarpēji paralēlas locījuma līnijas a un c.
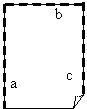
Caur punktu
ārpus locījuma līnijas ir iespējams uzlocīt tikai vienu locījuma līniju, kas
paralēla dotajai. To var izdarīt šādā veidā:
1. Ir dota taisne a un punkts
A, kas neatrodas uz a.
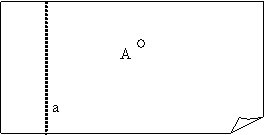
2. Pārloka lapu pa doto locījuma līniju a. Pārloka iegūto locījuma līniju caur doto punktu A, t.i., noloka dotajai locījuma līnijai perpendikulu b caur doto punktu. Tagad punkts A atrodas uz jaunās locījuma līnijas b.
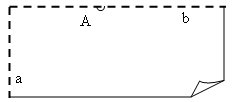
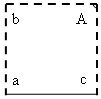
3. Locījuma līniju b vēlreiz pārloka “uz pusēm” caur doto punktu A, t.i., noloka locījuma līnijai b perpendikulāru locījuma līniju c caur punktu A.
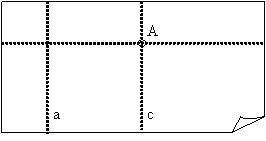
4. Atlokot vaļā papīra lapu, var redzēt, ka caur punktu A ārpus locījuma līnijas a ir uzlocīta dotajai paralēla locījuma līnija c. Ir uzlocīta dotajai locījuma līnijai paralēla locījuma līnija. Paralelitāte seko no locīšanas konstrukcijas.

Ceļvedis stereometrijas sākumam 11.klasei
Matemātikas paraugprogrammā temats saukts kā „Paralelitāte un perpendikularitāte telpā”.
Galvenā doma ir tāda, ka skolēnam jāsaprot, ka mūsu dzīve notiek trīsdimensiju telpā, kur praktiskos uzdevumus risina, galvenokārt, ar planimetrijas zināšanām. Pārmērīga kavēšanās pie stereometrijas kursa aksiomātiska izklāsta nav lietderīga ( līdzīgi kā daudz laika nevajag veltīt pamatskolā tikai ģeometriskiem pārveidojumiem, 10.klasē – spriedumiem un slēdzieniem), labāk jaunos stereometrijas jēdzienus apgūt, aplūkojot konkrētus ģeometriskos ķermeņus apkārtējā vidē un modeļos.
1. Materiāls „PLAKNE un TAISNES” dod īsu pārskatu par galvenajiem jēdzieniem stereometrijā. Lietderīga atziņa : „ Par teorēmu pareizību var pārliecināties arī praktiski, uztverot papīra lapu par plakni un locījuma līnijas par taisnēm.”
3. Stereometrijas pamatjēdzieni, paralelitāte un perpendikularitāte telpā
1. Stereometrijas aksiomas un secinājumi no tām
1.aksioma Caur jebkuriem diviem
punktiem var novilkt vienu vienīgu taisni.
No 1.aksiomas seko, ka jebkuri divi punkti viennozīmīgi nosaka taisni.
2.aksioma Caur jebkuriem trim telpas punktiem, kas neatrodas uz vienas taisnes,
var novilkt vienu vienīgu plakni.
No 2.aksiomas seko, ka jebkuri trīs punkti, kas neatrodas uz vienas taisnes,
viennozīmīgi nosaka plakni.
3.aksioma Ja divi taisnes punkti pieder plaknei, tad visi šīs taisnes punkti
pieder plaknei.
No 3.aksiomas seko, ka taisne atrodas plaknē (plakni var novilkt caur taisni)
tikai tad, ja taisnei un plaknei ir divi vai vairāki kopīgi punkti.
4.aksioma Ja divām plaknēm ir kopīgs punkts, tad tām ir kopīga taisne, uz kuras
atrodas visi šo plakņu kopīgie punkti.
No 4.aksiomas seko, ka plaknēm ir vai nu bezgalīgi daudz, vai arī nav neviena
kopīga punkta.
2.
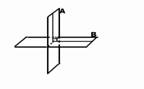
Taisnes var būt savstarpēji paralēlas,
krustiskas, perpendikulāras, šķērsas
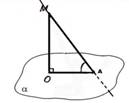
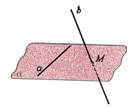
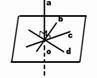
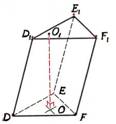
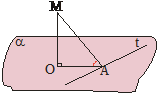
3. Par leņķi starp taisni un plakni sauc leņķi starp taisni un tās projekciju plaknē (ÐOAM)
Ja taisne ir perpendikulāra plaknei, tad uzskatīsim, ka leņķis starp šo taisni un plakni ir 90°, bet, ja taisne ir paralēla plaknei, tad uzskatīsim, ka leņķis starp šo taisni un plakni ir 0°.
4.
Taisne un plakne var būt paralēlas,
perpendikulāras, krustojošas, šķeļošas
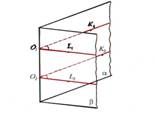
5. Plaknes var būt paralēlas, perpendikulāras, šķeļošas (krustojošas)
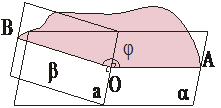
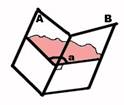
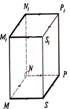
6. Divplakņu kakts
Par divplakņu kaktu sauc figūru, kuru veido divas pusplaknes ar kopīgu robežu, ja abas pusplaknes neatrodas vienā plaknē.
|
Abas pusplaknes α un β sauc par divplakņu kakta skaldnēm, bet kopīgo robežu jeb ierobežojošo taisni a – par divplakņu kakta šķautni. Uz divplakņu kakta šķautnes a
izvēlas punktu O. Abās pusplaknēs α un β novelk attiecīgus starus
OA |
|
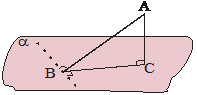
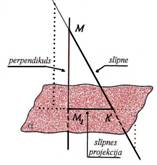
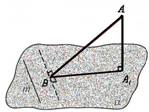
7. Triju perpendikulu teorēma
|
Ja taisne, kas atrodas plaknē, ir perpendikulāra pret slīpnes projekciju, tad tā ir perpendikulāra arī pret pašu slīpni.
AB – slīpne; BC – slīpnes
projekcija plaknē α. BC |
|
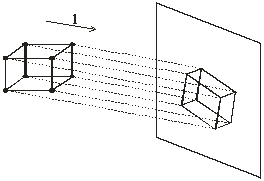
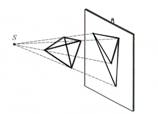
8. Telpisku figūru attēlošanas pamatprincipi plaknē ir paralēlā un centrālā projekcija
Telpisku figūru attēlošanu plaknē sauc par projicēšanu.
Plakni, uz kuras figūras attēlo, sauc par projekciju jeb zīmējuma plakni, bet izveidoto zīmējumu – par projekciju.
|
|
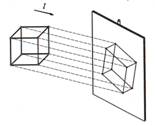
Ja kuba modeli novieto saules staros pret telpas sienu, uz sienas veidojas ēna. Šo ēnu var uzskatīt par kuba attēlu plaknē. Līdzīgi var iegūt kuba attēlu uz ekrāna, novietojot to ekrāna priekšā un apgaismojot ar paralēlu staru kūli, kurš iet virzienā l. |
Ja visu projicējošo staru virziens ir paralēls kādai taisnei, tad šo projicēšanas metodi sauc par paralēlo projicēšanu, šo taisni sauc par projicēšanas virzienu, bet iegūto attēlu – par paralēlo projekciju.
Paralēlo projekciju īpašības:
· Taisnes paralēlā projekcija ir taisne vai punkts.
· Paralēlā projicēšanā taisnes nogriežņu attiecība ir vienāda ar projekciju attiecību.
· Paralēlā projicēšanā paralēlu taišņu projekcijas ir paralēlas taisnes vai punkti.
· Paralēlā projicēšanā paralēlu taišņu nogriežņu attiecība ir vienāda ar projekciju attiecību.
|
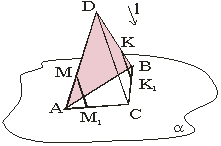
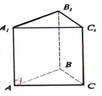
Trijstūra attēls paralēlajā
projekcijā plaknē: Par telpā dota trijstūra paralēlo projekciju zīmējuma plaknē var uzskatīt jebkuru trijstūri.
Trijstūra ADB projekcija plaknē α ir trijstūris ABC. |
|
|
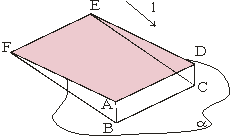
Paralelograma attēls
paralēlajā projekcijā plaknē: Par telpā dota paralelograma paralēlo projekciju zīmējuma plaknē var uzskatīt jebkuru paralelogramu.
Paralelograma ADEF projekcija plaknē α ir paralelograms BCEF. |
|
|
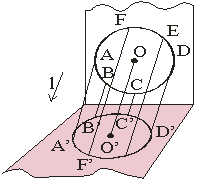
Riņķa līnijas attēls
paralēlajā projekcijā plaknē: Telpā dotas riņķa līnijas attēls paralēlajā projekcijā ir elipse.
Riņķa līnijas ar centru punktā O projekcija plaknē α ir riņķa līnijas ar centru punktā O’. |
|
Ja visi projicējošie stari iziet no viena punkta, tad šo projicēšanas metodi sauc par centrālo projicēšanu, šo punktu sauc par projicēšanas centru, bet iegūto attēlu – par telpiskās figūras centrālo projekciju.
9.
Pieci regulāri daudzskaldņi: tetraedrs, oktaedrs, heksaedrs,
ikosaedrs, dodekaedrs
Par tetraedru (regulāru četrskaldni) sauc ķermeni, kuru ierobežo četri
vienādi regulāri trijstūri. (tam ir 6 šķautnes un 4 virsotnes)
Par oktaedrs (regulāru astoņskaldni) sauc ķermeni, kuru ierobežo astoņi
regulāri trījstūri. (tam ir 12 šķautnes un 6 virsotnes)
Par heksaedru jeb kubu (regulāru sešskaldni) sauc ķermeni, kuru ierobežo
seši vienādi kvadrāti. (tam ir 12 šķautnes un 8 virsotnes)
Par ikosaedrs (regulāru divdesmitskaldni) sauc ķermeni, kuru ierobežo
divdesmit regulāri trijstūri. (tam ir 30 šķautnes un 12 virsotnes)
Par dodekaedru (regulāru divpadsmitskaldni) sauc ķermeni, kuru ierobežo
divpadsmit regulāri piecstūri. (tam ir 30 šķautnes un 20 virsotnes)
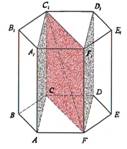
10. Daudzskaldņus var šķelt ar plakni
|
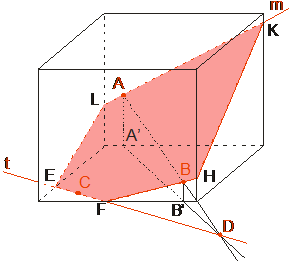
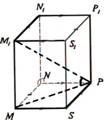
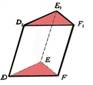
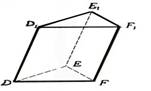
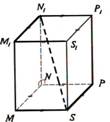
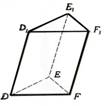
Piemērs. Konstruēt kuba šķēlumu ar plakni, ja dots viens šķēluma plaknes punkts apakšējā pamata plaknē un pa vienam šķēluma plaknes punktam divās pretējās sānu skaldnēs. Dotos punktus apzīmēsim ar A, B un C. Tad punkta A projekcija kuba pamata plaknē ir A´, punkta B projekcija ir punkts B´ (punkta C projekcija C´ sakrīt ar pašu punktu C). Savienosim punktus A un B ar taisni, savienosim arī šo punktu projekcijas A´ un B´ ar taisni un atradīsim šo taišņu krustpunktu D. Punkts D atrodas uz taisnes AB, tātad D ir šķēluma plaknes punkts, bet D atrodas arī uz taisnes A´B´ - tātad D ir arī pamata plaknes punkts (3. aksioma). Arī punkts C pieder gan šķēluma plaknei, gan pamata plaknei. Tāpēc šķēluma plakne šķeļas ar pamata plakni pa taisni CD (jeb CD ir šķēluma plaknes pēda pamata plaknē). Taisne CD krusto kuba pamata šķautnes punktos E un F. Tā kā F un B atrodas vienā skaldnē, tad, tos savienojot ar taisni, iegūstam šķēluma nogriezni FH. Tā kā kuba pretējās sānu skaldnes ir paralēlas, tad tās šķeļas ar šķēlējplakni pa paralēliem nogriežņiem. Tāpēc caur punktu A vilksim taisni m paralēli taisnei FH. Taisne m krusto kuba sānu šķautnes punktos K un L. Savienosim katrā sānu skaldnē iegūtos punktus: E un L, K un H. Iegūtais piecstūris EFHKL ir meklētais kuba šķēlums ar plakni. |
|
|
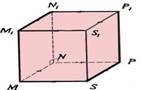
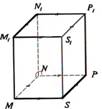
Divas taisnes sauc par paralēlām, ja tās atrodas vienā plaknē un nekrustojas (piemēram, AD||BC; EF||HG). Divas taisnes sauc par krustiskām, ja tām ir tikai viens kopīgs punkts (piemēram, AB krustiska ar BC; EH ar HG utt.). Divas taisnes sauc par perpendikulārām,
ja leņķis starp tām ir 90° (piemēram,
FE Divas taisnes sauc par šķērsām taisnēm, ja tās neatrodas vienā plaknē (piemēram, CG šķērsa ar AB; FE ar AD utt.). |
|
|
Taisni un plakni sauc par paralēlām, ja tās nekrustojas. Uzskata, ka jebkura taisne, kas atrodas plaknē, ir arī šai plaknei paralēla. |
|
|
Taisni sauc par perpendikulāru plaknei, ja tā ir perpendikulāra katrai šīs plaknes taisnei. |
|
|
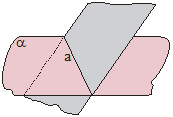
Taisne un plakne ir krustojošas, ja tām ir viens kopīgs punkts. Ja divām plaknēm ir kopīga taisne, tad saka, ka šīs plaknes šķeļas pa šo taisni jeb šī ir plakņu šķēluma taisne. |
|
Plaknes sauc par paralēlām, ja tās nešķeļas. Uzskata, ka katra plakne ir paralēla pati sev.
Divas plaknes sauc par perpendikulārām, ja leņķis starp tām ir 90°.
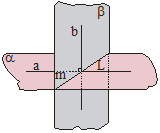
Plaknes sauc par šķeļošām, ja tām ir viens kopīgs punkts (plaknēm ir kopīga taisne).