Stereometrijas pamati
2. Īsi par plakni un taisni, to savstarpējo novietojumu.
Ja punkts pieder taisnei vai plaknei, t. i., punkts atrodas uz taisnes vai atrodas plaknē, tad teiksim arī, ka caur punktu var novilkt taisni vai plakni jeb – taisne vai plakne iet caur šo punktu.
Ja taisne pieder plaknei, t. i., taisne atrodas plaknē, tad teiksim arī, ka caur taisni var novilkt plakni jeb – plakne iet caur šo taisni.
1. AKSIOMA
Caur jebkuriem diviem telpas punktiem var novilkt vienu vienīgu taisni.
2. AKSIOMA
Caur jebkuriem trim telpas punktiem, kas neatrodas uz vienas taisnes, var novilkt vienu vienīgu plakni.
3. AKSIOMA
Ja divi taisnes punkti pieder plaknei, tad visi šīs taisnes punkti pieder plaknei.
4. AKSIOMA
Ja divām plaknēm ir kopīgs punkts, tad tām ir kopīga taisne, uz kuras atrodas visi šo plakņu kopīgie punkti.
PLAKNES NOVILKŠANA
(caur taisni un punktu;
caur divām krustiskām taisnēm)
1. TEORĒMA
Caur taisni un punktu, kas tai nepieder, var novilkt vienu vienīgu plakni.
![]()
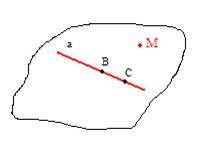
2. TEORĒMA
Caur divām krustiskām taisnēm var novilkt vienu vienīgu plakni.
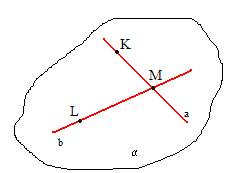
1. uzd.
Taisnes c un d krustojas punktā A, turklāt c atrodas plakne y.
Vai ir pareizs apgalvojums, ka a) taisne d atrodas plaknē y;
b) punkts A atrodas plaknē y?
2. uzd.
Pierādīt, ka caur taisni var novilkt bezgalīgi daudz plakņu.
TAIŠŅU PARALITĀTE
Definīcija
Divas taisnes sauc par paralēlēm, ja tās atrodas vienā plaknē un nekrustojas.
1. TEORĒMA
Caur divām paralēlām taisnēm var novilkt vienu vienīgu plakni.
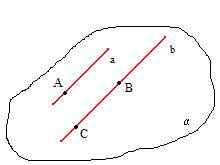
2. TEORĒMA
Telpā caur punktu ārpus taisnes var novilkt vienu vienīgu taisni, kas paralēla dotajai.
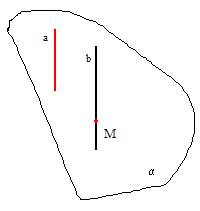
3. TEORĒMA
Ja viena no divām paralēlām taisnēm krusto plakni, tad arī otra taisne krusto šo plakni.
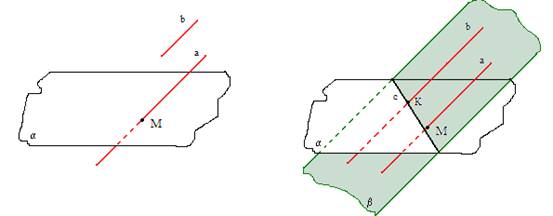
4. TEORĒMA
Ja katra no divām taisnēm ir paralēla trešajai taisnei, tad tās abas ir savstarpēji paralēlas.
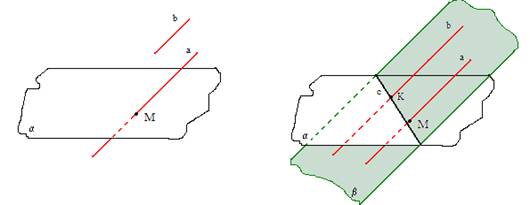
1. uzd.
Taisne ir paralēla vienai regulāra astoņstūra malai. Cik astoņstūra diagonālēm šī taisne ir paralēla?
2. uzd.
Dotas trīs paralēlas taisnes. Cik plakņu var novilkt tā, lai tās saturētu vismaz divas no dotajām taisnēm?
TAISNES un PLAKNES PARALELITĀTE
Definīcija
Taisni un plakni sauc par paralēlām, ja tās nekrustojas.
1. TEORĒMA (taisnes un plaknes paralelitātes pazīme)
Ja taisne, kas neatrodas plaknē, ir paralēla kādai šīs plaknes taisnei, tad tā ir paralēla pašai plaknei.
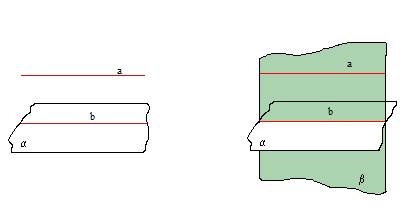
2. TEORĒMA
Ja plakne iet caur taisni, kas ir paralēla citai plaknei, un abas plaknes šķeļas, tad dotā taisne ir paralēla plakņu šķēluma taisnei.
1. uzd.
Rombs ABCD un taisnstūris CDEF atrodas dažādās plaknēs. Noteikt, kāda figūra ir četrstūris AEFB.
2. uzd.
Trapeces sānu malas viduspunktos krustojas ar plakni y. Pierādīt, ka trapeces pamati ir paralēli plaknei y.
PLAKŅU PARALITĀTE
Definīcija
Plaknes sauc par paralēlām, ja tās nešķeļas.
1.TEORĒMA
Ja kāda taisne krusto vienu no paralēlām plaknēm, tad tā krusto arī otru plakni.
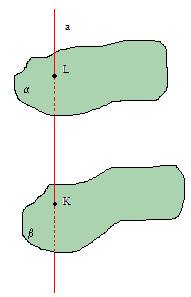
2. TEORĒMA
Ja kāda plakne šķeļ vienu no paralēlām plaknēm, tad tā šķeļ arī otru plakni.
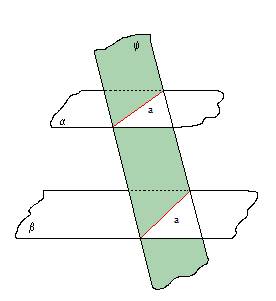
3. TEORĒMA (plakņu paralelitātes pazīme)
Ja vienas plaknes divas krustiskas taisnes ir attiecīgi paralēlas ar otras plaknes divām krustiskām taisnēm, tad šīs plaknes ir paralēlas.
4. TEORĒMA
Ja divas paralēlas plaknes šķeļ trešā plakne, tad plakņu šķēlumu taisnes ir paralēlas.
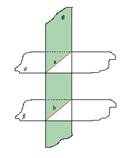
5. TEORĒMA
Paralēlu taišņu nogriežņi, kas atrodas starp paralēlām plaknēm, ir vienādi.
6. TEORĒMA
Caur punktu, kas neatrodas plaknē, var novilkt vienu vienīgu plakni, kas paralēla dotajai.
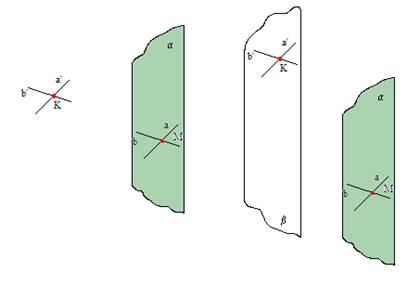
1. uzd.
Taisnes atrodas vienā no paralēlajām plaknēm. Pierādīt, ka taisne ir paralēla otrai plaknei.
2. uzd.
Trijstūra divas malas ir paralēlas plaknei y. Pierādīt, ka trijstūra trešā mala arī ir paralēla plaknei y.
ŠĶĒRSAS TAISNES
Definīcija
Divas taisnes sauc par šķērsām taisnēm, ja tās neatrodas vienā plaknē.
1. TEORĒMA (šķērsu taišņu pazīme)
Ja viena no divām taisnēm atrodas plaknē, bet otra taisne krusto šo plakni punktā, kas atrodas uz pirmās taisnes, tad dotās taisnes ir šķērsas.
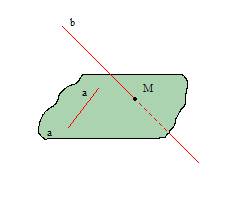
2. TEORĒMA
Caur katru no divām šķērsām taisnēm var novilkt vienu vienīgu plakni, kas ir paralēla otrai plaknei.
1. uzd.
Dots kubs ABCDAA’B’C’D’. Noteikt šādu taišņu savstarpējo stāvokli:
a) AB un D’C’;
b) BC un DD’;
c) AA’ un A’D’;
d) AC un D’B’.
2. uzd.
Taisne m iet caur kvadrāta ABCD centru O. Noteikt taišņu m un AD savstarpējo stāvokli, ja
a) m neatrodas kvadranta plaknē;
b) m atrodas kvadranta plaknē un krusto malu BC;
c) m krusto kvadrāta malas AB un CD to viduspunktos.
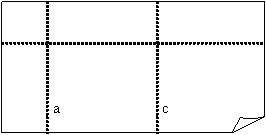
Par teorēmu pareizību var pārliecināties arī praktiski, uztverot papīra lapu par plakni un locījuma līnijas par taisnēm.
Divas taisnes
plaknē, kurām ir viens kopīgs punkts, sauc par krustiskām taisnēm.
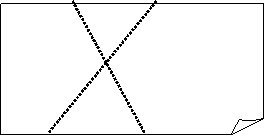
Krustisku taišņu locīšana:
1. Pārloka papīra lapu un
atloka to vaļā.
2. Veic vēl vienu locījumu
tā, lai jaunā locījuma līnija krustotos ar iepriekš uzlocīto. Papīra lapu
atloka vaļā. Var redzēt, ka ir uzlocītas divas krustiskas taisnes.
Šobrīd ierobežotā papīra lapa rada problēmu, jo ir iespējama tāda situācija, ka šīs taisnes ir krustiskas, bet tās krustojas ārpus lapas malām. Šeit ir jāpieņem, ka lapa ir neierobežota. Pārbaudīt, vai taisnes krustosies, var, pārbaudot, vai taisnes nav paralēlas. Ja taisnes nav paralēlas, tad tās ir krustiskas. Taišņu paralelitāti aplūkosim mazliet vēlāk.
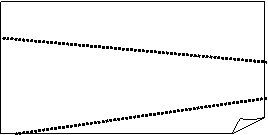
Krustiskas taisnes,
kuras krustojoties veido taisnu leņķi, sauc par perpendikulārām taisnēm.
Perpendikulāru taišņu
locīšana:
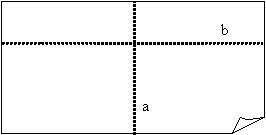
1. Pārloka papīra lapu pa
vēlamo locījuma līniju a, pret kuru vēlas novilkt perpendikulāru taisni.
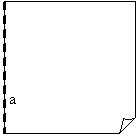
3. Pārloka locījuma līniju a “uz pusēm”. Ja perpendikulārā locījuma līnija jānoloka pret konkrētu punktu, tad pārloka locījuma līniju caur šo punktu.

3. Atlokot vaļā papīra lapu, var redzēt, ka ir nolocītas divas savstarpēji perpendikulāras locījuma līnijas a un b.
Divas dažādas
taisnes plaknē, kuras nekrustojas, sauc par paralēlām. Lai varētu uzlocīt divas paralēlas
taisnes, tiek izmantotas perpendikulāras taisnes.
Paralēlu taišņu locīšana:
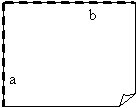
1. Sākumā locīšanu veic tādā
pašā veidā, kā lokot perpendikulāras taisnes. Konstruē divas perpendikulāras
locījuma līnijas a un b, bet papīra lapu neatloka vaļā (skat. perpendikulāru
taišņu locīšana 1., 2. punktu).
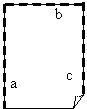
2. Pret locījuma līniju b noloka vēl vienu perpendikulāru locījuma līniju c, t.i., pārloka locījuma līniju.
3. Atlokot vaļā papīra lapu, var redzēt, ka ir uzlocītas divas savstarpēji paralēlas locījuma līnijas a un c.
Caur punktu
ārpus locījuma līnijas ir iespējams uzlocīt tikai vienu locījuma līniju, kas
paralēla dotajai. To var izdarīt šādā veidā:
1. Ir dota taisne a un punkts
A, kas neatrodas uz a.
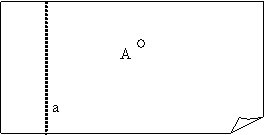
2. Pārloka lapu pa doto locījuma līniju a. Pārloka iegūto locījuma līniju caur doto punktu A, t.i., noloka dotajai locījuma līnijai perpendikulu b caur doto punktu. Tagad punkts A atrodas uz jaunās locījuma līnijas b.
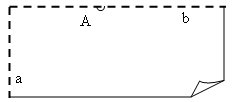
3. Locījuma līniju b vēlreiz pārloka “uz pusēm” caur doto punktu A, t.i., noloka locījuma līnijai b perpendikulāru locījuma līniju c caur punktu A.
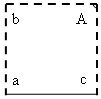
4. Atlokot vaļā papīra lapu, var redzēt, ka caur punktu A ārpus locījuma līnijas a ir uzlocīta dotajai paralēla locījuma līnija c. Ir uzlocīta dotajai locījuma līnijai paralēla locījuma līnija. Paralelitāte seko no locīšanas konstrukcijas.
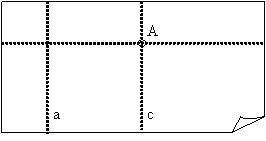

Ceļvedis stereometrijas sākumam 11.klasei
Matemātikas paraugprogrammā temats saukts kā „Paralelitāte un perpendikularitāte telpā”.
Galvenā doma ir tāda, ka skolēnam jāsaprot, ka mūsu dzīve notiek trīsdimensiju telpā, kur praktiskos uzdevumus risina, galvenokārt, ar planimetrijas zināšanām. Pārmērīga kavēšanās pie stereometrijas kursa aksiomātiska izklāsta nav lietderīga ( līdzīgi kā daudz laika nevajag veltīt pamatskolā tikai ģeometriskiem pārveidojumiem, 10.klasē – spriedumiem un slēdzieniem), labāk jaunos stereometrijas jēdzienus apgūt, aplūkojot konkrētus ģeometriskos ķermeņus apkārtējā vidē un modeļos.
1. Materiāls „PLAKNE un TAISNES” dod īsu pārskatu par galvenajiem jēdzieniem stereometrijā. Lietderīga atziņa : „ Par teorēmu pareizību var pārliecināties arī praktiski, uztverot papīra lapu par plakni un locījuma līnijas par taisnēm.”