Riņķis un daudzstūris mākslā, dabaszinātnēs un matemātikā. Skolotāja atbalsta materiāls.
7.stunda. Ievilktu un apvilktu daudzstūru elementu aprēķināšana.
12.uzdevums.
Veicot uzdevumu, skolēni:
- Attīstīs matemātisko valodu, lietos jēdzienus: apvilkts (ievilkts) trijstūris, četrstūris, sešstūris.
- Atkārtos zināmās formulas vai atradīs tās uzziņas literatūrā;
- Izteiks no formulas vajadzīgo lielumu.
- Izveidos pārskatu ar biežāk lietojamām formulām par ievilktiem un apvilktiem trijstūriem, četrstūriem, sešstūriem.
Ieteikumi skolotājam.
· Atkarībā no skolēnu spējām un atvēlētā laika, var aicināt papildināt tabulu ar sakarībām par ievilkta un apvilkta daudzstūra laukuma aprēķināšanu; var pierakstīt formulas, kas saista regulāra n-stūra malu ar ievilktas vai apvilktas riņķa līnijas rādiusu; var papildināt ar sakarībām, kā aprēķināt regulāra ievilkta un apvilkta daudzstūra leņķu lielumus.
· Stundas gaitā piedāvāt aprēķina uzdevumus, kuros lietot formulas regulāru apvilktu un ievilktu daudzstūru elementu aprēķināšanai.
Uzdevums. Aizpildi iesākto tabulu!
Sakarības starp regulāra daudzstūra malu garumu un ievilktas vai apvilktas riņķa līnijas rādiusu.
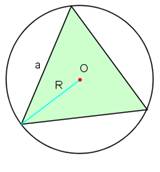
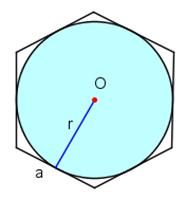
a – regulārā daudzstūra malas garums;
R – ap daudzstūri apvilktas riņķa līnijas rādiuss;
r – daudzstūrī ievilktas riņķa līnijas rādiuss.
|
Daudzstūra malu skaits |
Skaidrojums ar vārdiem |
Shematisks zīmējums |
Rādiuss (zināms malas garums) |
Malas garums (zināms rādiuss) |
|
3 |
Trijstūris ievilkts riņķī |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
Četrstūris apvilkts ap riņķa līniju |
|
|
a = 2r |
|
|
6 |
|
|
|
|
|
|
|
|
|