Riņķis un daudzstūris mākslā, dabaszinātnēs un matemātikā. Skolotāja atbalsta materiāls.

7.uzdevums.

Veicot uzdevumu, skolēni:

• atkārtos sakarības par ievilktu un centra leņķi;
• sadarbosies, strādājot viena varianta grupās;
• attīstīs matemātisko valodu, stāstos otram skolēnam savus risinājumus.

 

Ieteikumi skolotājam.

• Skolēni atkārto no pamatskolas par ievilktu un centra leņķi.
• Darba lapas 2 variantos. Pēc to aizpildīšanas, var izveidot vairākas 3 – 4 skolēnus grupas, kuriem bija 1.variants, un vairākas - 2.varianta. Skolēni šajās grupās salīdzina rezultātus 1.-5.uzdevumam, pārrunā atšķirības un nonāk līdz pareizam rezultātam. Tad skolēni apvienojas pāros, lai katrs būtu no sava varianta un izstāsta savus uzdevumu risinājumus otram skolēnam.
• Skolotājs var ievākt darba lapas, lai pārliecinātos par katra paša izveidoto uzdevumu atbilstību nosacījumiem. Tas dotu iespēju arī skolotājam pārliecināties par katra skolēna izpratni par ievilktu un centra leņķi.
• Nākamo stundu var iesākt, aktualizējot vēlreiz jautājumu par leņķiem riņķī un piedāvājot katram izpildīt divus cita skolēna izveidotos uzdevumus.

 

Darba lapa skolēnam

1.variants

Uzdevums.

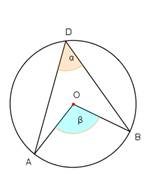
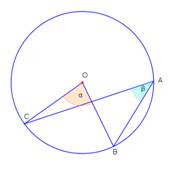
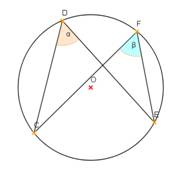
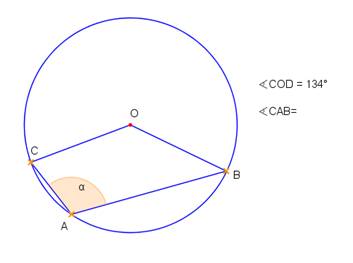
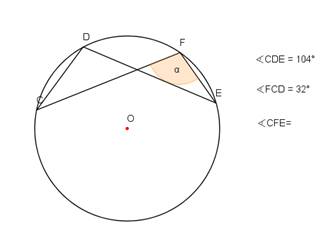
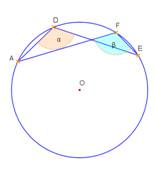
1. Noteikt sakarību starp leņķiem α un β  1. – 3. zīmējumā!
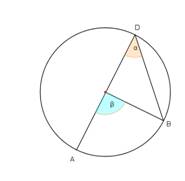
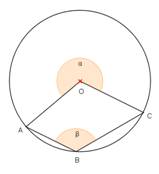
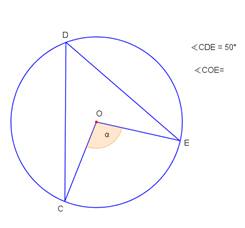
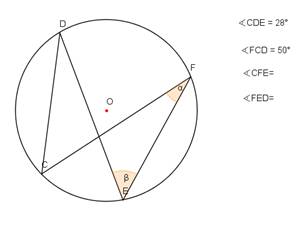
2. Noteikt leņķu lielumus 4. – 5.zīmējumā!
3. Izveidojiet divus savus uzdevumus, kuros būtu nepieciešams noteikt centra leņķus un ievilktus leņķus! Izveidojiet atbilstošus zīmējumus (6., 7.)!

Lenķi un riņķis

 

1.	2.	3.

 

4.	5.
6.	7.

Darba lapa skolēnam

2.variants

Uzdevums.

4. Noteikt sakarību starp leņķiem α un β  1. – 3. zīmējumā!
5. Noteikt leņķu lielumus 4. – 5.zīmējumā!
6. Izveidojiet divus savus uzdevumus, kuros būtu nepieciešams noteikt centra leņķus un ievilktus leņķus! Izveidojiet atbilstošus zīmējumus (6., 7.)!

Lenķi un riņķis

1.	2.	3.

 

4.	5.
6.	7.

8.uzdevums.

Veicot uzdevumu, skolēni:

• veidos aprakstam atbilstošu zīmējumu
• veiks loģiskus spriedumus, izmantojot sakarības trijstūros un par leņķiem riņķī;
• paskaidros katru darbību ar matemātiskiem pamatojumiem.

 

Ieteikumi skolotājam.

• Aicināt skolēnus veikt pēc apraksta pierādījumu, pa soļiem veidojot arī zīmējumu un pierakstot pamatojumu, vai un kāpēc tā drīkst darīt.. Tas varētu skolēnus veiksmīgāk atrast kļūdu.
• Vajadzētu īpaši uzslavēt skolēnus, kuri atrod kļūdu, jo pašam izdarīt pareizi ir vienkāršāk nekā atrast kļūdu cita risinājumā.

 

Uzdevums.

Kāds 1.kursa audzēknis, kurš tikko sācis mācīties tematu par riņķi un ar to saistītajiem nogriežņiem, ierodas nākamajā matemātikas stundā un svinīgi paziņo, ka viņš nepiekrīt skolotāja iepriekšējās stundas stāstījumam par hordu un diametru, jo viņš, lūk, pierādīja pavisam ko citu. Un tā viņa apgalvojums un pierādījums ir šāds.

 

Horda, kas neiet caur riņķa līnijas centru ir vienāda ar šī riņķa diametru!

Pierādījums.

1) Novelkam riņķa līnijas diametru AB.

2) Caur punktu B novelkam hordu BC, kas neiet caur riņķa līnijas centru.

3) Caur hordas BC viduspunktu D un punktu A novelkam jaunu hordu AE.

4) Savienojam ar nogriezni punktus E un C.

5) Apskatām trijstūrus ABD un EDC.

Pēc konstrukcijas BD = DC.

.

Ja viena trijstūra mala un divi leņķi ir vienādi ar otra trijstūra malu un diviem leņķiem, tad šie trijstūri ir savstarpēji vienādi.

Tātad ∆BDA=∆EDC. No tā varam secināt, ka AB = EC, tātad jebkura horda riņķī ir vienādā garumā ar diametru.

 

Kur skolēns kļūdījās? Izveido aprakstam atbilstošu zīmējumu, paskaidro, kur viņš kļūdījās un izlabo kļūdu viņa apgalvojumā!

 

9.uzdevums.

Veicot uzdevumu, skolēni:

• saskata zīmējumā ievilktus leņķus;
• lieto zināšanas par ievilktiem leņķiem, kas balstās uz diametru.

 

 

Ieteikumi skolotājam.

• Var izmantot materiālā piedāvāto Geonext failu un izveidot skolēniem individuālus zīmējumus, saglabājot ideju par ievilktiem leņķiem, kas balstās uz diametru.
• Var demonstrēt attēlu uz interaktīvās tāfeles, parādot dažādus novietojumus, uzsverot ka kādi no leņķiem visās situācijās saglabājas taisni.

 

Uzdevums.

Attēlā dots riņķis ar centru O un vairāki leņķi.

• Kuri riņķī iezīmētie leņķi ir taisni?
• Atzīmējiet tos, lietojot atbilstošu simboliku!
• Pamatojiet, kāpēc jūsu iezīmētie leņķi ir taisni!