Roberts Škapars. Pilnīga konkurence, monopols, monopolstiskā konkurence un oligopols. Teorija. (e-grāmata)
6.3.2. Peļņa pilnīgas konkurences apstākļos
Viens no svarīgākajiem uzņēmuma darbības rādītājiem ir peļņa π. To aprēķina, ja no uzņēmumā saražotā produkta realizācijas ieņēmumiem R atskaita kopējās izmaksas TC:
(6.3.1) π = R – TC; R – TC > 0.
Turpmāk pieņemsim, ka uzņēmējs cenšas iegūt maksimāli lielu peļņu.
(6.3.2) ![]()
Iepriekš noskaidrots, ka pilnīgas konkurences tirgū produkta vienības pārdošanas cena ir nemainīga.
Ja pārdošanas cena ir nemainīga (![]() ), ieņēmumu vienādojuma
), ieņēmumu vienādojuma
(6.3.3) R = P · Q
ģeometriskais attēls ir taisne. Tās kāpumu nosaka attiecība:
![]()
un to sauc par robežieņēmumiem (MR).
Saskaņā ar izteiksmi (6.3.3) vienādojumu (6.3.1)var pierakstīt šādi:
(6.3.4) ![]()
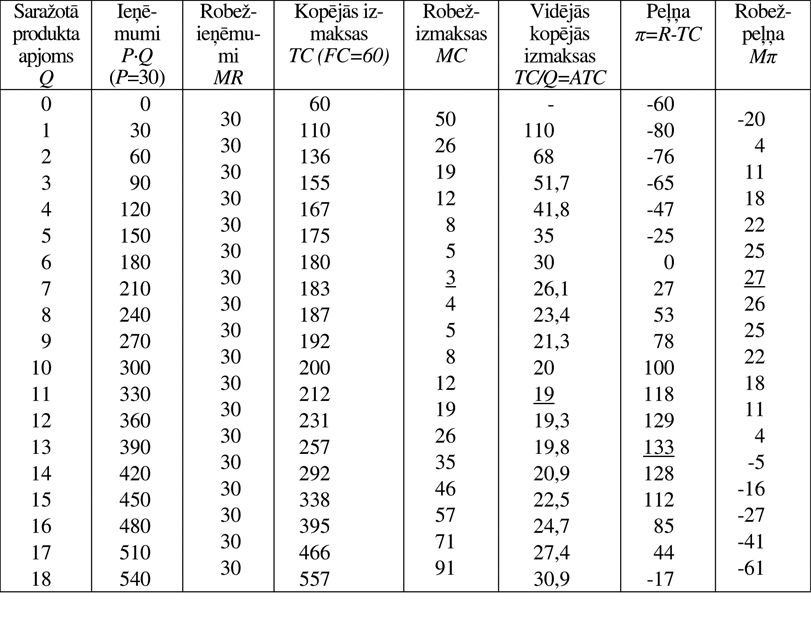
Izmantojot 6.3.1. tabulas datus, ieņēmumu taisni un kopējo izmaksu līkni var attēlot vienā koordinātu plaknē (6.3.1. attēls a). Izmaksu līknei ir tāda pati forma kā apakšnodaļā apskatītajai. 6.3.1. attēla a diagrammā var redzēt, ka, ražojot produkta apjomus 6 un 17, uzņēmums ar ieņēmumiem R sedz tikai kopējās izmaksas TC un negūst peļņu
(6.3.5) π= R – TC =0,
tāpēc punktus A0 un A’0 sauc par produkta ražošanas kritiskajiem punktiem. Piemēram, ja Q<6 un saražotā produkta kopējais apjoms ir 4, uzņēmums strādās ar zaudējumiem (ar nogriežņa A3A4 skaitlisko vērtību). Punkts A2 ir ieņēmumu funkcijai paralēli novilktas taisnes T1 un izmaksu līknes pieskaršanās punkts. Tā projekcija uz abscisu ass rāda saražotā produkta kopējo apjomu (Q=1), kura ražošana pie esošās tirgus cenas rada uzņēmumam vislielākos zaudējumus. To lielums ir vienāds ar nogriežņa A1A2 skaitlisko vērtību Savukārt, ja Q>6 un saražotā produkta kopējais apjoms ir, piemēram, 8, uzņēmums gūs peļņu (kas ir vienāda ar nogriežņa A5A6 skaitlisko vērtību). Maksimālā peļņa ir vienāda ar nogriežņa A7A8 skaitlisko vērtību, jo punkts A7 ir ieņēmumu taisnei paralēli novilktas taisnes T2 un izmaksu līknes pieskaršanās punkts. Tā projekcija uz abscisu ass rāda to saražotā produkta kopējo apjomu, kurš uzņēmumam nodrošina maksimālo peļņu (Q=13). Tādējādi starp kritiskajiem punktiem A0 un A’0 veidojas peļņas lauks (6.3.1. attēls a, b). Tā lielums un pastāvēšanas iespēja ir atkarīga no līkņu R un TC formas un to izvietojuma koordinātu plaknē.
6.3.1. Maksimālās peļņas noteikšana pilnīgas konkurences tirgū
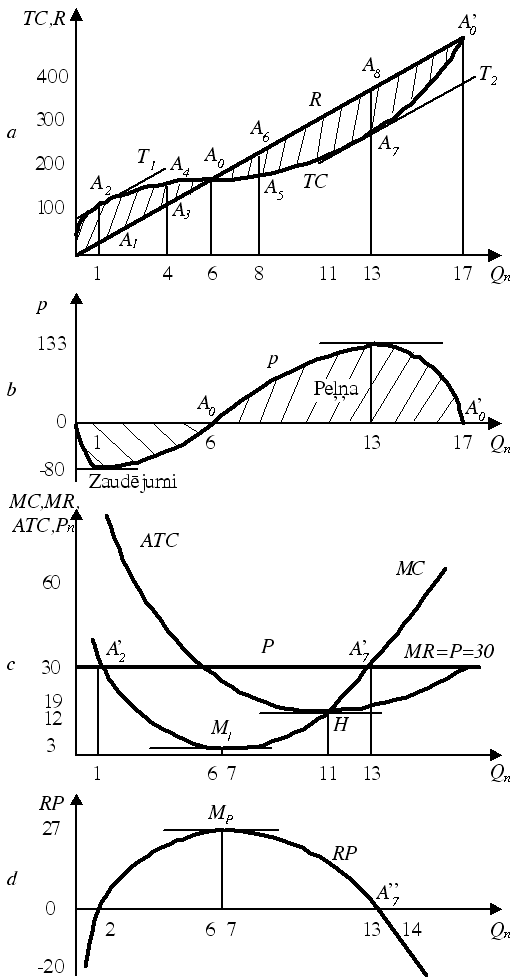
6.3.1. attēls. Peļņas maksimizācija pilnīgā konkurencē:
a – ieņēmumi un kopējās izmaksas; b – peļņa; c – robežizmaksas,
robežieņēmumi, vidējās izmaksas; d – robežpeļņa
Maksimālās peļņas sasniegšanas nosacījumus var atspoguļot arī ar pieprasījuma π robežieņēmu MR un robežizmaksu MC līknēm, kuras, izmantojot 6.3.1. tabulas datus, ir parādītas 6.3.1. attēlā c. Ieņēmumu pieaugumu raksturo robežieņēmumu taisne, kas ir paralēla abscisu asij un ir vienāda ar tirgus cenu 30. Robežizmaksu līknei šajā gadījumā ir U veida forma. Sākumā robežizmaksas samazinās, jo samazinās izmaksu pieaugums, līdz kļūst vienādas ar tirgus cenu (punkts A’2). Robežizmaksām kļūstot mazākām par tirgus cenu, zaudējumi sāk samazināties un peļņa pieaug. Peļņas pieaugumu raksturo robežpeļņa Mπ (6.3.1. attēls d) ![]()
Tā rāda, kā palielinās peļņa, ja produkta ražošana pieaug par vienu vienību. Robežpeļņas līknei Mπ ir apgriezta U veida forma. Augot robežpeļņai, uzņēmumam ir izdevīgi paplašināt ražošanu. Robežizmaksas (6.3.1. attēls c) turpina samazināties līdz minimālajai vērtībai 3 punktā MI. Vienlaikus robežpeļņa punktā MP sasniedz maksimālo vērtību 27, jo cena un robežieņēmumi ir konstanti. Robežizmaksām palielinoties, robežpeļņa vienlaikus samazinās. Robežizmaksu, robežieņēmumu un cenas (pieprasījuma) līkņu krustpunktā A’7 Q=13 uzņēmums gūs maksimālo peļņu (piemērā – 133 vienības). Turpinot palielināt produkta ražošanu, papildu izmaksu summa būs lielāka nekā ieņēmumu pieaugums un līdz ar to peļņa samazināsies.
Tātad peļņas maksimizāciju pilnīgā konkurencē var definēt šādi: uzņēmums gūst maksimālo peļņu, ja tas ražo tādu produkta apjomu, kurš atrodas robežizmaksu pieaugošā zara apgabalā un kura robežizmaksas ir vienādas ar preces tirgus cenu.
(6.3.6) P = MC
Šeit ir uzsvērta robežizmaksu līknes pieaugošā zara nozīme, jo arī tās samazinošamies skaitlisko nozīmju zaram ir krustpunkts ar robežieņēmumu taisni
(A’2), taču tajā tiek sasniegta nevis maksimālā peļņa, bet gan maksimālie zaudējumi.
Ja pieņemam, ka tirgus cena samazinās līdz c=10, ievērojot iepriekšējos definīcijas noteikumus, uzņēmumam būtu jāražo tāds produkta daudzums, kas nodrošina vienādojuma (6.3.6) nosacījumus. Taču šāda cena ir mazāka par vidējo kopējo izmaksu funkcijas minimālo vērtību 19. Tas nozīmē, ka netiks segtas vienas produkta vienības izmaksas, tāpēc ražošanu ir vēlams turpināt, kad tirgus cenas minimālais līmenis Pmin = ATCmin = 19 vienības. Tādā gadījumā tiks segtas vienas produkcijas vienības izmaksas. Gadījumos, kad tirgus cena ir zemāka par minimālo cenu (P<Pmin), uzņēmums var izmantot vēl vienu paņēmienu zaudējumu samazināšanai vai pat peļņas gūšanai, ja starpība Pmin- P1 nav liela. Tā kā ražošanas process ir atkarīgs galvenokārt no mainīgajām izmaksām, tad uzņēmums īslaicīgi var atteikties no pastāvīgo izmaksu kompensēšanas. Tādā gadījumā uzņēmuma darbību vairs neatspoguļo ATC līkne, bet gan AVC līkne, kura koordinātu sistēmā parasti atrodas zemāk par ATC līkni, līdz ar to, punktam H un Pmin pārvietojoties uz leju līdz H’ atbilstoši pazeminātai cenai P’min , uzņēmums gūst īslaicīgu iespēju turpināt produkcijas ražošanu un nepasliktināt savu ekonomisko stāvokli (6.3.2. attēls).
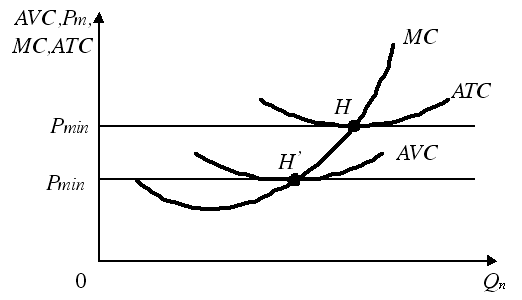
6.3.2. attēls. Peļņas maksimizācija pilnīgā konkurencē, ja uzņēmums īslaicīgi nemaksā pastāvīgās izmaksas
Punktu H, kurā vidējo kopējo izmaksu minimums un robežizmaksas ir vienādas, sauc par optimālo izmaksu punktu. Tam atbilst vienādojums
(6.3.7) ATC=MC.
Piemērā tas sasniegts, ražojot 11 produkta vienības. Šī ražošanas apjoma gadījumā ATC=MC=19.
Apkopojot analīzes rezultātus, secināms, ka uzņēmuma īsā laika piedāvājuma līkne ir robežizmaksu līknes MC pieaugošā zara posms virs vidējo mainīgo izmaksu AVC līknes.