Stereometrijas pamati

3. Stereometrijas pamatjēdzieni, paralelitāte un perpendikularitāte telpā

 

1.      Stereometrijas aksiomas un secinājumi no tām

1.aksioma Caur jebkuriem diviem punktiem var novilkt vienu vienīgu taisni.
No 1.aksiomas seko, ka jebkuri divi punkti viennozīmīgi nosaka taisni.
2.aksioma Caur jebkuriem trim telpas punktiem, kas neatrodas uz vienas taisnes, var novilkt vienu vienīgu plakni.
No 2.aksiomas seko, ka jebkuri trīs punkti, kas neatrodas uz vienas taisnes, viennozīmīgi nosaka plakni.
3.aksioma Ja divi taisnes punkti pieder plaknei, tad visi šīs taisnes punkti pieder plaknei.
No 3.aksiomas seko, ka taisne atrodas plaknē (plakni var novilkt caur taisni) tikai tad, ja taisnei un plaknei ir divi vai vairāki kopīgi punkti.
4.aksioma Ja divām plaknēm ir kopīgs punkts, tad tām ir kopīga taisne, uz kuras atrodas visi šo plakņu kopīgie punkti.
No 4.aksiomas seko, ka plaknēm ir vai nu bezgalīgi daudz, vai arī nav neviena kopīga punkta.

2.      Taisnes var būt savstarpēji paralēlas, krustiskas, perpendikulāras, šķērsas

3.      Par leņķi starp taisni un plakni sauc leņķi starp taisni un tās projekciju plaknē (ÐOAM)

Ja taisne ir perpendikulāra plaknei, tad uzskatīsim, ka leņķis starp šo taisni un plakni ir 90°, bet, ja taisne ir paralēla plaknei, tad uzskatīsim, ka leņķis starp šo taisni un plakni ir 0°.

4.      Taisne un plakne var būt paralēlas, perpendikulāras, krustojošas, šķeļošas

5.      Plaknes var būt paralēlas, perpendikulāras, šķeļošas (krustojošas)

 

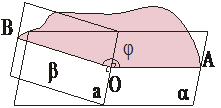
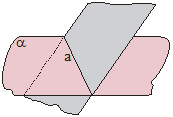
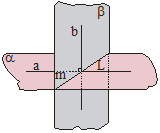
6.      Divplakņu kakts

Par divplakņu kaktu sauc figūru, kuru veido divas pusplaknes ar kopīgu robežu, ja abas pusplaknes neatrodas vienā plaknē.

Abas pusplaknes α un β sauc par divplakņu kakta skaldnēm, bet kopīgo robežu jeb ierobežojošo taisni a – par divplakņu kakta šķautni. Uz divplakņu kakta šķautnes a izvēlas punktu O. Abās pusplaknēs α un β novelk attiecīgus starus OAa un OBa. Iegūto leņķi AOB sauc par divplakņu kakta leņķi.

 

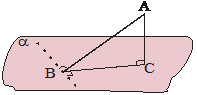
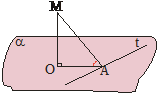
7.      Triju perpendikulu teorēma

Ja taisne, kas atrodas plaknē, ir perpendikulāra pret slīpnes projekciju, tad tā ir perpendikulāra arī pret pašu slīpni.   AB – slīpne; BC – slīpnes projekcija plaknē α. BCtaisnes, kas atrodas plaknē α.

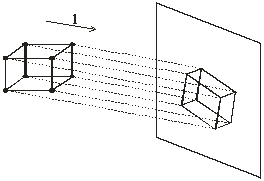
8.      Telpisku figūru attēlošanas pamatprincipi plaknē ir paralēlā un centrālā projekcija

Telpisku figūru attēlošanu plaknē sauc par projicēšanu.

Plakni, uz kuras figūras attēlo, sauc par projekciju jeb zīmējuma plakni, bet izveidoto zīmējumu – par projekciju.

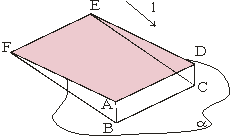
Ja kuba modeli novieto saules staros pret telpas sienu, uz sienas veidojas ēna. Šo ēnu var uzskatīt par kuba attēlu plaknē. Līdzīgi var iegūt kuba attēlu uz ekrāna, novietojot to ekrāna priekšā un apgaismojot ar paralēlu staru kūli, kurš iet virzienā l.

 

Ja visu projicējošo staru virziens ir paralēls kādai taisnei, tad šo projicēšanas metodi sauc par paralēlo projicēšanu, šo taisni sauc par projicēšanas virzienu, bet iegūto attēlu – par paralēlo projekciju.

Paralēlo projekciju īpašības:

·         Taisnes paralēlā projekcija ir taisne vai punkts.

·         Paralēlā projicēšanā taisnes nogriežņu attiecība ir vienāda ar projekciju attiecību.

·         Paralēlā projicēšanā paralēlu taišņu projekcijas ir paralēlas taisnes vai punkti.

·         Paralēlā projicēšanā paralēlu taišņu nogriežņu attiecība ir vienāda ar projekciju attiecību.

 

Trijstūra attēls paralēlajā projekcijā plaknē: Par telpā dota trijstūra paralēlo projekciju zīmējuma plaknē var uzskatīt jebkuru trijstūri.   Trijstūra ADB projekcija plaknē α ir trijstūris ABC.
Paralelograma attēls paralēlajā projekcijā plaknē: Par telpā dota paralelograma paralēlo projekciju zīmējuma plaknē var uzskatīt jebkuru paralelogramu.   Paralelograma ADEF projekcija plaknē α ir paralelograms BCEF.
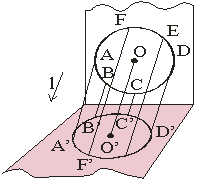
Riņķa līnijas attēls paralēlajā projekcijā plaknē: Telpā dotas riņķa līnijas attēls paralēlajā projekcijā ir elipse.   Riņķa līnijas ar centru punktā O projekcija plaknē α ir riņķa līnijas ar centru punktā O’.

 

Ja visi projicējošie stari iziet no viena punkta, tad šo projicēšanas metodi sauc par centrālo projicēšanu, šo punktu sauc par projicēšanas centru, bet iegūto attēlu – par telpiskās figūras centrālo projekciju.

9.            Pieci regulāri daudzskaldņi: tetraedrs, oktaedrs, heksaedrs, ikosaedrs, dodekaedrs
Par tetraedru (regulāru četrskaldni) sauc ķermeni, kuru ierobežo četri vienādi regulāri trijstūri. (tam ir 6 šķautnes un 4 virsotnes)
Par oktaedrs (regulāru astoņskaldni) sauc ķermeni, kuru ierobežo astoņi regulāri trījstūri. (tam ir 12 šķautnes un 6 virsotnes)
Par heksaedru jeb kubu (regulāru sešskaldni) sauc ķermeni, kuru ierobežo seši vienādi kvadrāti. (tam ir 12 šķautnes un 8 virsotnes)
Par ikosaedrs (regulāru divdesmitskaldni) sauc ķermeni, kuru ierobežo divdesmit regulāri trijstūri. (tam ir 30 šķautnes un 12 virsotnes)
Par dodekaedru (regulāru divpadsmitskaldni) sauc ķermeni, kuru ierobežo divpadsmit regulāri piecstūri. (tam ir 30 šķautnes un 20 virsotnes)

 

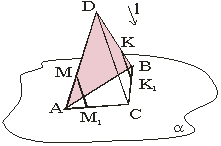
10.         Daudzskaldņus var šķelt ar plakni

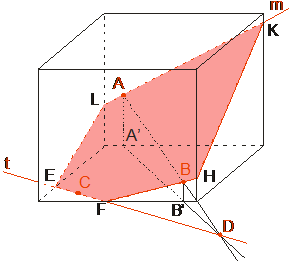
Piemērs. Konstruēt kuba šķēlumu ar plakni, ja dots viens šķēluma plaknes punkts apakšējā pamata plaknē un pa vienam šķēluma plaknes punktam divās pretējās sānu skaldnēs. Dotos punktus apzīmēsim ar A, B un C. Tad punkta A projekcija kuba pamata plaknē ir A´, punkta B projekcija ir punkts B´ (punkta C projekcija C´ sakrīt ar pašu punktu C). Savienosim punktus A un B ar taisni, savienosim arī šo punktu projekcijas A´ un B´ ar taisni un atradīsim šo taišņu krustpunktu D. Punkts D atrodas uz taisnes AB, tātad D ir šķēluma plaknes punkts, bet D atrodas arī uz taisnes A´B´ - tātad D ir arī pamata plaknes punkts (3. aksioma). Arī punkts C pieder gan šķēluma plaknei, gan pamata plaknei. Tāpēc šķēluma plakne šķeļas ar pamata plakni pa taisni CD (jeb CD ir šķēluma plaknes pēda pamata plaknē). Taisne CD krusto kuba pamata šķautnes punktos E un F. Tā kā F un B atrodas vienā skaldnē, tad, tos savienojot ar taisni, iegūstam šķēluma nogriezni FH. Tā kā kuba pretējās sānu skaldnes ir paralēlas, tad tās šķeļas ar šķēlējplakni pa paralēliem nogriežņiem. Tāpēc caur punktu A vilksim taisni m paralēli taisnei FH. Taisne m krusto kuba sānu šķautnes punktos K un L. Savienosim katrā sānu skaldnē iegūtos punktus: E un L, K un H. Iegūtais piecstūris EFHKL ir meklētais kuba šķēlums ar plakni.

 

 

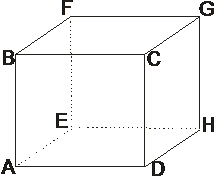
Divas taisnes sauc par paralēlām, ja tās atrodas vienā plaknē un nekrustojas (piemēram, AD||BC; EF||HG). Divas taisnes sauc par krustiskām, ja tām ir tikai viens kopīgs punkts (piemēram, AB krustiska ar BC; EH ar HG utt.). Divas taisnes sauc par perpendikulārām, ja leņķis starp tām ir 90° (piemēram, FEEH; FEFB utt.). Divas taisnes sauc par šķērsām taisnēm, ja tās neatrodas vienā plaknē (piemēram, CG šķērsa ar AB; FE ar AD utt.).

 

 

1.  

Taisni un plakni sauc par paralēlām, ja tās nekrustojas. Uzskata, ka jebkura taisne, kas atrodas plaknē, ir arī šai plaknei paralēla.
Taisni sauc par perpendikulāru plaknei, ja tā ir perpendikulāra katrai šīs plaknes taisnei.
Taisne un plakne ir krustojošas, ja tām ir viens kopīgs punkts. Ja divām plaknēm ir kopīga taisne, tad saka, ka šīs plaknes šķeļas pa šo taisni jeb šī ir plakņu šķēluma taisne.

 

 

 

2.  

Plaknes sauc par paralēlām, ja tās nešķeļas. Uzskata, ka katra plakne ir paralēla pati sev.

Divas plaknes sauc par perpendikulārām, ja leņķis starp tām ir 90°.

Plaknes sauc par šķeļošām, ja tām ir viens kopīgs punkts (plaknēm ir kopīga taisne).