Roberts Škapars. Pieprasījuma un piedāvājums elastības. Teorija. (e-grāmata)

3.1. Elastības jēdziens

2.1. un 2.2. apakšnodaļās jau apskatīta dažādu lielumu iedarbība uz pieprasījumu un piedāvājumu, kura dažādām precēm var būt atšķirīga. Ir derīgi zināt tās intensitāti. Iedarbības pakāpi var noteikt aptuveni pēc pieprasījuma vai piedāvājuma līknes kāpuma. Jo lēzenāka ir līkne, jo preces pieprasījuma (piedāvājuma) pārmaiņas, apskatāmajam ietekmējošam lielumam mainoties, ir lielākas. Tomēr šāds iedarbības noteikšanas veids nav precīzs, tāpēc ka līkne dažādos tās posmos var būt ar atšķirīgu kāpumu. Turklāt uzdevumu sarežģī tas, ka dažādas preces uz ietekmējošo lielumu pārmaiņām reaģē dažādi, arī preces mērvienību dimensijas nav vienādas. Piemēram, graudu piedāvājumu mēra centneros un cenu – latos par vienu centneru; to nevar salīdzināt ar vieglo automobiļu piedāvājumu gabalos un cenu latos par vienu gabalu. Tāpēc ir nepieciešams ietekmējošo lielumu iedarbības mērs, kas der visām precēm un ļauj tās savstarpēji salīdzināt. Šāds mērs ir elastība. Ar to tiek raksturota nevis absolūtu, bet relatīvu lielumu izmaiņu attiecība. Piemēram, benzīna viena litra cenas 15 santīmi palielinājums par 5 santīmiem ir ļoti jūtama izmaiņa, taču benzīna mucas cenas tāds pats pieaugums ir maznozīmīgs.

Elastība ir bezdimensiju lielums, un visbiežāk tiek aprēķināta procentos. Viena no elastības raksturīgākām iezīmēm ir tā, ka vairākumā gadījumu to var noteikt ne visai apskatāmā lieluma līknei kopumā, bet gan kādam tās konkrētam punktam. Elastības kvantitatīvais mērs ir elastības koeficients e_y, kuru nosaka šādi:

(3.1.1) 

vai arī

(3.1.2) 

Tātad elastība ir lielums, kas rāda, par cik procentiem mainās pētāmais lielums, ja ietekmējošais lielums mainās par vienu procentu.

Apzīmējot pētāmo lielumu ar x un tā izmaiņas ar Δx, ietekmējošo lielumu ar y un tā izmaiņas ar Δy, iegūstam

(3.1.3)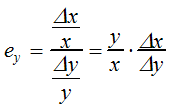  

Elastība var būt gan pozitīva, gan negatīva. Tas atkarīgs no pieprasījuma (piedāvājuma) līknes kāpuma. Elastībai ir pozitīvs koeficients, ja līknei ir pozitīvs kāpums, un negatīvs, ja līknes kāpums ir negatīvs. Attiecība Δx/Δy raksturo arī līknes stāvumu (3.1.1. attēls). Jo tā ir mazāka, jo stāvāka ir arī līkne. Līkne, kura koordinātu plaknē veidojas ar kāpumu no labās apakšējās malas uz kreiso augšējo malu (3.1.1. attēls a), tiek uzskatīta par līkni ar negatīvu kāpumu, un otrādi, līkne, kurai kāpums koordinātu plaknē ir no apakšējās kreisās malas uz augšējo labo malu (3.1.1. attēls b), tiek uzskatīta par līkni ar pozitīvu kāpumu. Matemātiski to izsaka šādi:

• ja Δx/Δy < 0 , tad līknei ir negatīvs kāpums,

• ja Δx/Δy > 0 , tad līknei ir pozitīvs kāpums,

kur Δx uz abscisu ass atliktā pētāmā lieluma izmaiņas un Δy ir uz ordinātu ass atliktā ietekmējošā lieluma izmaiņas.

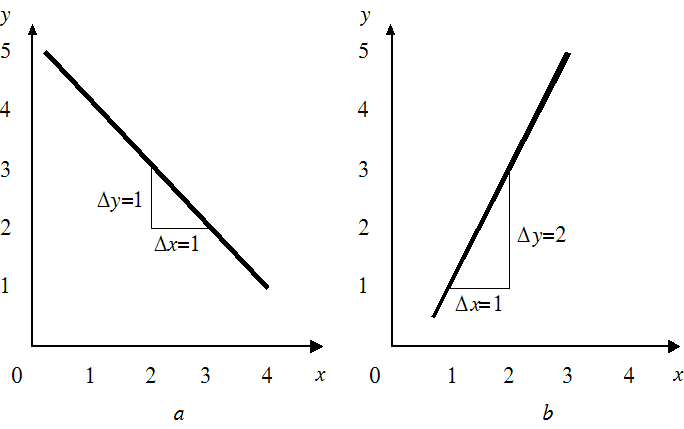
3.1.1. attēls. Līkne: a – ar negatīvu kāpumu; b – ar pozitīvu kāpumu